Kartesisches Produkt

Das kartesische Produkt oder Mengenprodukt ist in der Mengenlehre eine grundlegende Konstruktion, aus gegebenen Mengen eine neue Menge zu erzeugen. Gelegentlich wird für das kartesische Produkt auch die mehrdeutige Bezeichnung „Kreuzprodukt“ verwendet. Das kartesische Produkt zweier Mengen ist die Menge aller geordneten Paare von Elementen der beiden Mengen, wobei die erste Komponente ein Element der ersten Menge und die zweite Komponente ein Element der zweiten Menge ist. Allgemeiner besteht das kartesische Produkt mehrerer Mengen aus der Menge aller Tupel von Elementen der Mengen, wobei die Reihenfolge der Mengen und damit der entsprechenden Elemente fest vorgegeben ist. Die Ergebnismenge des kartesischen Produkts wird auch Produktmenge, Kreuzmenge oder Verbindungsmenge genannt. Das kartesische Produkt ist nach dem französischen Mathematiker René Descartes benannt, der es zur Beschreibung des kartesischen Koordinatensystems verwendete und damit die analytische Geometrie begründete.

Produkt zweier Mengen

Definition

Das kartesische Produkt ${\displaystyle A\times B}$ (lies „A kreuz B“) zweier Mengen ${\displaystyle A}$ und ${\displaystyle B}$ ist definiert als die Menge aller geordneten Paare ${\displaystyle (a,b)}$, wobei ${\displaystyle a}$ ein Element aus ${\displaystyle A}$ und ${\displaystyle b}$ ein Element aus ${\displaystyle B}$ ist. Dabei wird jedes Element aus ${\displaystyle A}$ mit jedem Element aus ${\displaystyle B}$ kombiniert. Formal ist das kartesische Produkt durch

${\displaystyle A\times B:=\left\{(a,b)\mid a\in A,b\in B\right\}}$

definiert. Insbesondere ist es auch möglich, das kartesische Produkt einer Menge mit sich selbst zu bilden und man schreibt dann

${\displaystyle A^{2}=A\times A=\left\{(a,a')\mid a,a'\in A\right\}}$.

Gelegentlich wird für das kartesische Produkt auch der Begriff „Kreuzprodukt“ verwendet, der jedoch weitere Bedeutungen hat, siehe Kreuzprodukt.

Die obige Definition ist problemlos auf (echte) Klassen ${\displaystyle A}$ und ${\displaystyle B}$ erweiterbar. Insbesondere erfolgt die Paarbildung nur für Elemente von ${\displaystyle A}$ und ${\displaystyle B}$; diese können keine echten Klassen sein und stellen an die Paarbildung keine besonderen Anforderungen.

Beispiele

Endliche Mengen

Das kartesische Produkt ${\displaystyle A\times B}$ der beiden Mengen ${\displaystyle A=\{a,b,c\}}$ und ${\displaystyle B=\{x,y\}}$ ist

${\displaystyle A\times B=\left\{(a,x),(a,y),(b,x),(b,y),(c,x),(c,y)\right\}}$.

Das kartesische Produkt ${\displaystyle B\times A}$ ist hingegen eine andere Menge, und zwar

${\displaystyle B\times A=\left\{(x,a),(x,b),(x,c),(y,a),(y,b),(y,c)\right\}}$,

da bei geordneten Paaren die Reihenfolge der Elemente eine Rolle spielt. Das kartesische Produkt von ${\displaystyle A}$ mit sich selbst ist

${\displaystyle A\times A=\left\{(a,a),(a,b),(a,c),(b,a),(b,b),(b,c),(c,a),(c,b),(c,c)\right\}}$.

Reelle Zahlen

Die reelle Zahlenebene entsteht aus dem kartesischen Produkt der reellen Zahlen ${\displaystyle \mathbb {R} }$ mit sich selbst:

${\displaystyle \mathbb {R} \times \mathbb {R} =\mathbb {R} ^{2}=\{(x,y)\mid x,y\in \mathbb {R} \}}$.

Intervalle

Die Tupel ${\displaystyle (x,y)}$ nennt man auch kartesische Koordinaten. Das kartesische Produkt zweier reeller Intervalle ${\displaystyle [a,b]}$ und ${\displaystyle [c,d]}$ ergibt das Rechteck

${\displaystyle [a,b]\times [c,d]=\{(x,y)\in \mathbb {R} ^{2}\mid a\leq x\leq b,c\leq y\leq d\}}$.

Spielkarten

Spielkarten, wie sie zum Beispiel beim Texas Hold’em, beim Canasta, beim Doppelkopf und beim Skat verwendet werden, sind ein Beispiel für ein kartesisches Produkt. Die erste Menge ist in diesem Fall die Menge der Kartenwerte, zum Beispiel V = {A, K, Q, J, 10, 9, 8, 7, 6, 5, 4, 3, 2}, und die zweite Menge ist die Menge der Kartensymbole, zum Beispiel S = {♣, ♠, ♥, ♦}. Die Menge der Spielkarten ist dann das kartesische Produkt dieser beiden Mengen: V × S = {(A, ♣), (A, ♠), (A, ♥), (A, ♦), (K, ♣), ..., (3, ♦), (2, ♣), (2, ♠), (2, ♥), (2, ♦)}.

In diesem Beispiel hat die Menge ${\displaystyle V}$ der Kartenwerte 13 Elemente, also ${\displaystyle |V|=13}$, und die Menge ${\displaystyle S}$ der Kartensymbole hat 4 Elemente, also ${\displaystyle |S|=4}$. Daraus ergibt sich, dass die Menge ${\displaystyle V\times S}$ der Spielkarten ${\displaystyle |V\times S|=|V|\cdot |S|=13\cdot 4=52}$ Elemente hat.

Dieses kartesische Produkt kann mit einer Tabelle dargestellt werden:

kartesisches Produkt aus Kartenwerten und Kartensymbolen
${\displaystyle V\times S}$	♣	♠	♥	♦
A	(A, ♣)	(A, ♠)	(A, ♥)	(A, ♦)
K	(K, ♣)	(K, ♠)	(K, ♥)	(K, ♦)
Q	(Q, ♣)	(Q, ♠)	(Q, ♥)	(Q, ♦)
J	(J, ♣)	(J, ♠)	(J, ♥)	(J, ♦)
10	(10, ♣)	(10, ♠)	(10, ♥)	(10, ♦)
...	...	...	...	...
3	(3, ♣)	(3, ♠)	(3, ♥)	(3, ♦)
2	(2, ♣)	(2, ♠)	(2, ♥)	(2, ♦)

U-Bahnlinien oder S-Bahnlinien

Bei Verkehrsnetzen, die aus U-Bahnlinien und S-Bahnlinien bestehen, ist die Menge der Verkehrslinien ein kartesisches Produkt, das zum Beispiel aus der Menge L = {U, S} der Linienarten und der Menge N = {1, 2, 3, 4, 5, 6, 7} der Liniennummern gebildet werden kann. Hier ist ${\displaystyle |L\times N|=|L|\cdot |N|=2\cdot 7=14}$.

kartesisches Produkt aus Linienarten (U/S-Bahnlinien) und Liniennummern
${\displaystyle L\times N}$	1	2	3	4	5	6	7
	U1	U2	U3	U4	U5	U6	U7
	S1	S2	S3	S4	S5	S6	S7

Hinweise:

Es ergibt sich nur dann ein (vollständiges) kartesisches Produkt, wenn die Anzahl der U-Bahnlinien und S-Bahnlinien gleich ist. Ansonsten ergibt sich ein unvollständiges kartesisches Produkt, das grundsätzlich andere Eigenschaften hat. Im Bereich der Informatik und Programmierung ist dieses Thema zum Beispiel unter Array - Dimensionen zu finden.

Eigenschaften

Zahl der Elemente

Sind die Mengen ${\displaystyle A}$ und ${\displaystyle B}$ endlich, dann ist ihr kartesisches Produkt ${\displaystyle A\times B}$ eine endliche Menge geordneter Paare. Die Anzahl der Paare entspricht dabei dem Produkt der Anzahlen der Elemente der Ausgangsmengen, das heißt

${\displaystyle |A\times B|=|A|\cdot |B|}$

In dem Spezialfall, dass ${\displaystyle A=B}$ ist, gilt

${\displaystyle |A^{2}|=|A|^{2}}$.

Enthält zumindest eine der beiden Mengen ${\displaystyle A}$ und ${\displaystyle B}$ unendlich viele Elemente und ist die andere nicht leer, dann besteht ihr kartesisches Produkt ${\displaystyle A\times B}$ aus unendlich vielen Paaren. Das kartesische Produkt zweier abzählbar unendlicher Mengen ist dabei nach Cantors erstem Diagonalargument ebenfalls abzählbar. Ist zumindest eine der beiden Mengen überabzählbar, so ist auch ihre Produktmenge überabzählbar.

Leere Menge

Da aus der leeren Menge kein Element ausgewählt werden kann, ergibt das kartesische Produkt der leeren Menge mit einer beliebigen Menge wieder die leere Menge. Allgemeiner gilt

${\displaystyle A\times B=\emptyset ~\Longleftrightarrow ~A=\emptyset ~{\text{oder}}~B=\emptyset }$,

das heißt, das kartesische Produkt zweier Mengen ist genau dann leer, wenn zumindest eine der beiden Mengen leer ist.

Nichtkommutativität

Das kartesische Produkt ist nicht kommutativ, das heißt, für nichtleere Mengen ${\displaystyle A}$ und ${\displaystyle B}$ mit ${\displaystyle A\neq B}$ ist

${\displaystyle A\times B\neq B\times A}$,

denn in den Paaren der Menge ${\displaystyle A\times B}$ ist das erste Element aus ${\displaystyle A}$ und das zweite aus ${\displaystyle B}$, während in den Paaren der Menge ${\displaystyle B\times A}$ das erste Element aus ${\displaystyle B}$ und das zweite aus ${\displaystyle A}$ ist. Es gibt allerdings eine kanonische Bijektion zwischen den beiden Mengen, nämlich

${\displaystyle A\times B\to B\times A,\quad (a,b)\mapsto (b,a)}$,

mit der die Mengen miteinander identifiziert werden können.

Nichtassoziativität

Das kartesische Produkt ist auch nicht assoziativ, das heißt, für nichtleere Mengen ${\displaystyle A}$, ${\displaystyle B}$ und ${\displaystyle C}$ gilt im Allgemeinen

${\displaystyle A\times \left(B\times C\right)\neq \left(A\times B\right)\times C}$,

denn die Menge auf der linken Seite enthält Paare, deren erstes Element aus ${\displaystyle A}$ und deren zweites Element ein Paar aus ${\displaystyle B\times C}$ ist, wohingegen die Menge auf der rechten Seite Paare enthält, deren erstes Element ein Paar aus ${\displaystyle A\times B}$ und deren zweites Element aus ${\displaystyle C}$ ist. Auch hier gibt es eine kanonische Bijektion zwischen diesen beiden Mengen, nämlich

${\displaystyle A\times \left(B\times C\right)\to \left(A\times B\right)\times C,\quad (a,(b,c))\mapsto ((a,b),c)}$.

Manche Autoren identifizieren die Paare ${\displaystyle (a,(b,c))}$ und ${\displaystyle ((a,b),c)}$ mit dem geordneten Tripel ${\displaystyle (a,b,c)}$, wodurch das kartesische Produkt auch assoziativ wird.

Distributivität

Für das kartesische Produkt gelten die folgenden Distributivgesetze bezüglich Vereinigung, Schnitt und Differenzbildung von Mengen:

${\displaystyle {\begin{aligned}\left(A\cup B\right)\times C&=\left(A\times C\right)\cup \left(B\times C\right)\\\left(A\cap B\right)\times C&=\left(A\times C\right)\cap \left(B\times C\right)\\\left(A\setminus B\right)\times C&=\left(A\times C\right)\setminus \left(B\times C\right)\\A\times \left(B\cup C\right)&=\left(A\times B\right)\cup \left(A\times C\right)\\A\times \left(B\cap C\right)&=\left(A\times B\right)\cap \left(A\times C\right)\\A\times \left(B\setminus C\right)&=\left(A\times B\right)\setminus \left(A\times C\right)\end{aligned}}}$

Das vierte Gesetz kann verwendet werden, um die Distributivität bei den Natürlichen Zahlen zu beweisen, wenn diese über Kardinalzahlen definiert sind.

Monotonie und Komplement

Das kartesische Produkt verhält sich monoton bezüglich Teilmengenbildung, das heißt, sind die Mengen ${\displaystyle A_{1},A_{2},B_{1}}$ und ${\displaystyle B_{2}}$ nichtleer, dann gilt

${\displaystyle (A_{1}\times A_{2})\subseteq (B_{1}\times B_{2})~\Longleftrightarrow ~A_{1}\subseteq B_{1}~{\text{und}}~A_{2}\subseteq B_{2}}$.

Insbesondere gilt dabei Gleichheit

${\displaystyle (A_{1}\times A_{2})=(B_{1}\times B_{2})~\Longleftrightarrow ~A_{1}=B_{1}~{\text{und}}~A_{2}=B_{2}}$.

Betrachtet man die Menge ${\displaystyle B_{1}}$ als Grundmenge von ${\displaystyle A_{1}}$ und die Menge ${\displaystyle B_{2}}$ als Grundmenge von ${\displaystyle A_{2}}$, dann hat das Komplement von ${\displaystyle A_{1}\times A_{2}}$ in ${\displaystyle B_{1}\times B_{2}}$ die Darstellung

${\displaystyle (A_{1}\times A_{2})^{\mathsf {C}}=(A_{1}^{\mathsf {C}}\times A_{2}^{\mathsf {C}})\cup (A_{1}^{\mathsf {C}}\times A_{2})\cup (A_{1}\times A_{2}^{\mathsf {C}})}$.

Weitere Rechenregeln

Es gilt zwar

${\displaystyle \left(A_{1}\cap A_{2}\right)\times \left(B_{1}\cap B_{2}\right)=\left(A_{1}\times B_{1}\right)\cap \left(A_{2}\times B_{2}\right)}$,

aber im Allgemeinen ist

${\displaystyle \left(A_{1}\cup A_{2}\right)\times \left(B_{1}\cup B_{2}\right)\supseteq \left(A_{1}\times B_{1}\right)\cup \left(A_{2}\times B_{2}\right)}$,

da die Menge auf der linken Seite Paare aus ${\displaystyle A_{1}\times B_{2}}$ und ${\displaystyle A_{2}\times B_{1}}$ enthält, die in der Menge auf der rechten Seite nicht enthalten sind.

Produkt endlich vieler Mengen

Definition

Allgemeiner ist das kartesische Produkt ${\displaystyle A_{1}\times \dotsb \times A_{n}}$ von ${\displaystyle n}$ Mengen ${\displaystyle A_{1},\dotsc ,A_{n}}$ definiert als die Menge aller ${\displaystyle n}$-Tupel ${\displaystyle (a_{1},\dotsc ,a_{n})}$, wobei ${\displaystyle a_{i}}$ für ${\displaystyle i=1,\ldots ,n}$ jeweils ein Element aus der Menge ${\displaystyle A_{i}}$ ist. Formal ist das mehrfache kartesische Produkt durch

${\displaystyle A_{1}\times \dotsb \times A_{n}:=\left\{(a_{1},\dotsc ,a_{n})\mid a_{i}\in A_{i}~{\text{für}}~i=1,\dotsc ,n\right\}}$

definiert. Mit Hilfe des Produktzeichens wird das mehrfache kartesische Produkt auch durch

${\displaystyle \prod _{i=1}^{n}A_{i}=A_{1}\times \dotsb \times A_{n}}$

notiert. Das ${\displaystyle n}$-fache kartesische Produkt einer Menge ${\displaystyle A}$ mit sich selbst schreibt man auch als

${\displaystyle A^{n}=\underbrace {A\times \dotsc \times A} _{n{\text{-mal}}}=\left\{(a_{1},\dotsc ,a_{n})\mid a_{i}\in A~{\text{für}}~i=1,\dotsc ,n\right\}}$.

Leeres Produkt

Das kartesische Produkt von null Mengen ist die Menge, die als einziges Element das leere Tupel enthält, das heißt

${\displaystyle \prod _{i=1}^{0}A_{i}=\{()\}.}$

Insbesondere ist für eine beliebige Menge ${\displaystyle A}$

${\displaystyle A^{0}=\{()\}}$.

Davon wird Gebrauch gemacht, wenn Konstanten einer mathematischen Struktur als nullstellige Verknüpfungen betrachtet werden.

Vereinigung aller Produkte

Mit ${\displaystyle A^{*}}$ bezeichnet man die Vereinigung aller ${\displaystyle n}$-fachen kartesischen Produkte einer Menge ${\displaystyle A}$ mit sich selbst (für alle ${\displaystyle n\in \mathbb {N} }$), also die Menge aller Tupel mit Elementen aus A, einschließlich des leeren Tupels:

${\displaystyle A^{*}=\bigcup _{n=0}^{\infty }A^{n}}$.

Beispiele

Ist ${\displaystyle A=\left\{0,1\right\}}$, dann ist

${\displaystyle A\times A\times A=A^{3}=\{(0,0,0),(0,0,1),(0,1,0),(0,1,1),(1,0,0),(1,0,1),(1,1,0),(1,1,1)\}}$.

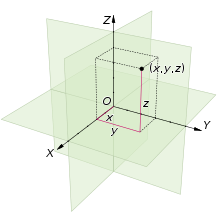
Der euklidische Raum ${\displaystyle \mathbb {R} ^{3}}$ besteht aus dem dreifachen kartesischen Produkt der reellen Zahlen ${\displaystyle \mathbb {R} }$:

${\displaystyle \mathbb {R} \times \mathbb {R} \times \mathbb {R} =\mathbb {R} ^{3}=\{(x,y,z)\mid x,y,z\in \mathbb {R} \}}$.

Die 3-Tupel ${\displaystyle (x,y,z)}$ sind die dreidimensionalen kartesischen Koordinaten. Das kartesische Produkt dreier reeller Intervalle ${\displaystyle [a,b]}$, ${\displaystyle [c,d]}$ und ${\displaystyle [e,f]}$ ergibt den Quader

${\displaystyle [a,b]\times [c,d]\times [e,f]=\{(x,y,z)\in \mathbb {R} ^{3}\mid a\leq x\leq b,c\leq y\leq d,e\leq z\leq f\}}$.

Allgemein ergibt das ${\displaystyle n}$-fache kartesische Produkt der reellen Zahlen den Raum ${\displaystyle \mathbb {R} ^{n}}$ und das kartesische Produkt von ${\displaystyle n}$ reellen Intervallen ein Hyperrechteck.

Eigenschaften

Zahl der Elemente

Sind die Mengen ${\displaystyle A_{1},\dotsc ,A_{n}}$ alle endlich, dann ist ihr kartesisches Produkt ebenfalls eine endliche Menge, wobei die Anzahl der Elemente von ${\displaystyle A_{1}\times \dotsb \times A_{n}}$ gleich dem Produkt der Elementzahlen der Ausgangsmengen ist, das heißt

${\displaystyle |A_{1}\times \dotsb \times A_{n}|=|A_{1}|\cdot \ldots \cdot |A_{n}|}$

bzw. in anderer Schreibweise

${\displaystyle \left|\prod _{i=1}^{n}A_{i}\right|=\prod _{i=1}^{n}|A_{i}|}$.

In dem Spezialfall, dass alle Mengen ${\displaystyle A_{i}}$ gleich einer Menge ${\displaystyle A}$ sind, gilt

${\displaystyle |A^{n}|=|A|^{n}}$.

Das kartesische Produkt endlich vieler abzählbar unendlicher Mengen ist ebenfalls abzählbar, wie sich durch Iteration des Arguments für das kartesische Produkt zweier Mengen mit Hilfe der Cantorschen Tupelfunktion zeigen lässt.

Monotonie

Sind die Mengen ${\displaystyle A_{1},\ldots ,A_{n}}$ und ${\displaystyle B_{1},\ldots ,B_{n}}$ nichtleer, dann gilt wie beim kartesischen Produkt zweier Mengen Monotonie

${\displaystyle \prod _{i=1}^{n}A_{i}\subseteq \prod _{i=1}^{n}B_{i}~\Longleftrightarrow ~A_{i}\subseteq B_{i}~{\text{für}}~i=1,\ldots ,n}$

und Gleichheit

${\displaystyle \prod _{i=1}^{n}A_{i}=\prod _{i=1}^{n}B_{i}~\Longleftrightarrow ~A_{i}=B_{i}~{\text{für}}~i=1,\ldots ,n}$.

Produkt unendlich vieler Mengen

Definition

Es ist auch möglich, das kartesische Produkt unendlich vieler Mengen zu definieren. Ist dazu ${\displaystyle I}$ eine Indexmenge und ${\displaystyle (A_{i})_{i\in I}}$ eine Familie von Mengen, dann definiert man das kartesische Produkt der Mengen ${\displaystyle A_{i}}$ durch

${\displaystyle \prod _{i\in I}A_{i}={\Big \{}f\colon I\to \bigcup _{i\in I}A_{i}\,{\Big |}\,\forall i\in I\colon f(i)\in A_{i}{\Big \}}}$.

Dies ist die Menge aller Abbildungen ${\displaystyle f}$ von ${\displaystyle I}$ in die Vereinigung der Mengen ${\displaystyle A_{i}}$, für die das Bild ${\displaystyle f(i)}$ in ${\displaystyle A_{i}}$ liegt. Sind alle ${\displaystyle A_{i}}$ gleich einer Menge ${\displaystyle A}$, dann ist das kartesische Produkt

${\displaystyle \prod _{i\in I}A=A^{I}}$

die Menge aller Funktionen von ${\displaystyle I}$ nach ${\displaystyle A}$. Sind die Mengen ${\displaystyle A_{i}}$ unterschiedlich, so ist das kartesische Produkt allerdings weit weniger anschaulich. Bereits die Frage, ob ein beliebiges kartesisches Produkt nichtleerer Mengen nichtleer ist, ist mit der Zermelo-Fraenkel-Mengenlehre ZF nicht entscheidbar; die Behauptung, dass es nichtleer ist, ist eine Formulierung des Auswahlaxioms, welches zu ZF hinzugefügt wird, um die Mengenlehre ZFC („Zermelo-Fraenkel + Choice“) zu erhalten.

Spezialfälle

Ein wichtiger Spezialfall eines unendlichen kartesischen Produkts entsteht durch die Wahl der natürlichen Zahlen ${\displaystyle \mathbb {N} }$ als Indexmenge. Das kartesische Produkt einer Folge von Mengen ${\displaystyle (A_{i})_{i\in \mathbb {N} }=(A_{1},A_{2},\ldots )}$

${\displaystyle \prod _{i=1}^{\infty }A_{i}=\left\{(a_{1},a_{2},\dotsc )\mid a_{i}\in A_{i}~{\text{für}}~i\in \mathbb {N} \right\}}$

entspricht dann der Menge aller Folgen, deren ${\displaystyle i}$-tes Folgenglied in der Menge ${\displaystyle A_{i}}$ liegt. Sind beispielsweise alle ${\displaystyle A_{i}=\mathbb {R} }$, dann ist

${\displaystyle \prod _{i=1}^{\infty }\mathbb {R} =\mathbb {R} \times \mathbb {R} \times \dotsb =\mathbb {R} ^{\mathbb {N} }=\left\{(a_{1},a_{2},\dotsc )\mid a_{i}\in \mathbb {R} ~{\text{für}}~i\in \mathbb {N} \right\}}$

die Menge aller reeller Zahlenfolgen. Das abzählbare kartesische Produkt lässt sich bijektiv auf das allgemein definierte kartesische Produkt abbilden, denn jede Folge ${\displaystyle (a_{1},a_{2},\dotsc )}$ definiert eine Funktion ${\displaystyle f}$ mit ${\displaystyle f(1):=a_{1},f(2):=a_{2},\dotsc }$ und umgekehrt lässt sich jede solche Funktion als Folge ${\displaystyle (f(1),f(2),\dotsc )}$ schreiben. Auch das kartesische Produkt endlich vieler Mengen lässt sich unter Verwendung endlicher Folgen als Spezialfall der allgemeinen Definition auffassen.

Universelle Eigenschaft des kartesischen Produktes

Zu dem kartesischen Produkt ${\displaystyle P=\prod \limits _{i\in I}A_{i}}$ gehört die Familie der Projektionen ${\displaystyle \pi _{i}\colon \prod \limits _{i\in I}A_{i}\ni \alpha \mapsto \alpha (i)\in A_{i}}$. Das kartesische Produkt ${\displaystyle \prod \limits _{i\in I}A_{i}}$ zusammen mit der Familie ${\displaystyle (\pi _{i}|i\in I)}$ hat die folgende Eigenschaft: Ist ${\displaystyle X}$ eine beliebige Menge und ist ${\displaystyle f_{i}\colon X\to A_{i}}$ eine Familie von Abbildungen, so gibt es genau eine Abbildung ${\displaystyle f\colon X\to \prod \limits _{i\in I}A_{i}}$ mit ${\displaystyle \pi _{i}\circ f=f_{i}}$ für alle ${\displaystyle i\in I}$. Das heißt, folgendes Diagramm ist kommutativ:

Ist ${\displaystyle Q}$ zusammen mit der Familie ${\displaystyle p_{i}\colon Q\to A_{i}}$ auch diese Eigenschaft, so gibt es eine bijektive Abbildung ${\displaystyle P\to Q}$.

Abgeleitete Begriffe

• Eine binäre Relation zwischen zwei Mengen ist eine Teilmenge des kartesischen Produkts der beiden Mengen. Insbesondere ist damit jede Abbildung eine Teilmenge des kartesischen Produkts aus Definitions- und Zielmenge der Abbildung. Allgemeiner ist eine ${\displaystyle n}$-stellige Relation eine Teilmenge des kartesischen Produkts von ${\displaystyle n}$ Mengen.
• Eine Projektion ist eine Abbildung von dem kartesischen Produkt zweier Mengen zurück in eine dieser Mengen. Allgemeiner ist eine Projektion eine Abbildung von dem kartesischen Produkt einer Familie von Mengen auf das kartesische Produkt einer Teilfamilie dieser Mengen, die Elemente mit bestimmten Indizes auswählt.
• Eine zweistellige Verknüpfung ist eine Abbildung von dem kartesischen Produkt zweier Mengen in eine weitere Menge. Allgemeiner ist eine ${\displaystyle n}$-stellige Verknüpfung eine Abbildung von dem kartesischen Produkt von ${\displaystyle n}$ Mengen in eine weitere Menge. Jede ${\displaystyle n}$-stellige Verknüpfung kann somit auch als ${\displaystyle (n+1)}$-stellige Relation aufgefasst werden.
• Ein direktes Produkt ist ein Produkt algebraischer Strukturen, wie zum Beispiel von Gruppen oder Vektorräumen, das aus dem kartesischen Produkt der Trägermengen besteht und zusätzlich mit ein oder mehreren komponentenweisen Verknüpfungen versehen ist. Eine direkte Summe ist eine Teilmenge des direkten Produkts, die sich nur für Produkte unendlich vieler Mengen vom direkten Produkt unterscheidet; sie besteht aus allen Tupeln, die nur an endlich vielen Stellen von einem bestimmten Element (meist dem neutralen Element einer Verknüpfung) verschieden sind.
• Das kategorielle Produkt entspricht in der Kategorie der Mengen dem kartesischen Produkt und in der Kategorie der Gruppen sowie in anderen Kategorien algebraischer Strukturen dem direkten Produkt.
• In relationalen Datenbanken werden das kartesische Produkt von Tabellen und die darauf aufbauenden Join-Operationen zur Verknüpfung von Datenbanktabellen eingesetzt.

Literatur

• Oliver Deiser: Einführung in die Mengenlehre. Die Mengenlehre Georg Cantors und ihre Axiomatisierung durch Ernst Zermelo. 2. verbesserte und erweiterte Auflage. Springer, Berlin u. a. 2004, ISBN 3-540-20401-6.
• M. Sh. Tsalenko: Direct product. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 1-55608-010-7 (englisch, encyclopediaofmath.org). 

Weblinks

• Eric W. Weisstein: Cartesian product. In: MathWorld (englisch).
• David Jao: Cartesian product. In: PlanetMath. (englisch)
• Thomas Foregger, David Jao, Andrew Archibald: Generalized cartesian product. In: PlanetMath. (englisch)