Koordinatentransformation

Bei einer Koordinatentransformation werden aus den Koordinaten, die ein Punkt in einem Koordinatensystem hat, die Koordinaten berechnet, die er in einem anderen Koordinatensystem hat. Formal gesehen ist dies die Umwandlung (Transformation) der ursprünglichen Koordinaten ${\displaystyle (x_{1},x_{2},\dotsc ,x_{n})}$ in die neuen Koordinaten ${\displaystyle (x'_{1},x'_{2},\dotsc ,x'_{n})}$. Die häufigsten Anwendungen finden sich in der Geometrie, der Geodäsie, der Photogrammetrie und bei technischen Aufgabenstellungen, aber auch in solch populären Bereichen wie der Computeranimation oder bei Computerspielen, in denen die dargestellte „Realität“ aus Sicht des Spielers, wenn er sich bewegt, fortwährend neu berechnet werden muss.

Typische Koordinatentransformationen entstehen durch Drehung (Rotation), Skalierung (Veränderung des Maßstabs), Scherung und Verschiebung (Translation) des Koordinatensystems, die auch kombiniert werden können.

Allgemein können die neuen Koordinaten ${\displaystyle x'_{i}}$ beliebige Funktionen der alten Koordinaten ${\displaystyle x_{i}}$ sein. In der Regel verwendet man spezielle Transformationen, bei denen diese Funktionen gewissen Einschränkungen – z. B. Differenzierbarkeit, Linearität oder Formtreue – unterliegen. Koordinatentransformationen können angewendet werden, wenn sich ein Problem in einem anderen Koordinatensystem leichter lösen lässt, z. B. bei der Transformation von kartesischen Koordinaten in Kugelkoordinaten oder umgekehrt.

Ein Spezialfall der Koordinatentransformation ist der Basiswechsel in einem Vektorraum.^[1]

Die hier betrachteten Transformationen, bei denen die Koordinatensysteme geändert werden und sich dadurch nur die Koordinaten der Punkte ändern, während die Punkte selbst unverändert bleiben, heißen auch passive oder Alias-Transformationen,^[2] während Transformationen, bei denen sich umgekehrt die Position der Punkte gegenüber einem festen Koordinatensystems ändert, auch aktive oder Alibi-Transformationen^[3] genannt werden (siehe Abb.).

Bei linearen Transformationen sind die neuen Koordinaten lineare Funktionen der ursprünglichen, also

${\displaystyle x'_{1}=a_{11}x_{1}+a_{12}x_{2}+\dots +a_{1n}x_{n}}$

${\displaystyle x'_{2}=a_{21}x_{1}+a_{22}x_{2}+\dots +a_{2n}x_{n}}$

${\displaystyle \ldots }$

${\displaystyle x'_{n}=a_{n1}x_{1}+a_{n2}x_{2}+\dots +a_{nn}x_{n}}$.

Dies kann man kompakt als Matrixmultiplikation des alten Koordinatenvektors ${\displaystyle {\vec {x}}=(x_{1},\dots ,x_{n})}$ mit der Matrix ${\displaystyle A}$, die die Koeffizienten ${\displaystyle a_{ij}}$ enthält, darstellen

${\displaystyle {\vec {x}}'=A{\vec {x}}}$.

Der Ursprung des neuen Koordinatensystems stimmt dabei mit dem des ursprünglichen Koordinatensystems überein.

Ein wichtiger Typ linearer Koordinatentransformationen sind solche, bei denen das neue Koordinatensystem gegenüber dem alten um den Koordinatenursprung gedreht ist (in nebenstehender Grafik die sogen. „Alias-Transformation“). In zwei Dimensionen gibt es dabei als Parameter lediglich den Rotationswinkel, im Dreidimensionalen dagegen muss weiters eine sich durch die Rotation nicht ändernde Drehachse definiert werden. Beschrieben wird die Drehung dabei in beiden Fällen durch eine Drehmatrix.

Betrachtet werden zwei dreidimensionale kartesische Koordinatensysteme ${\displaystyle S}$ und ${\displaystyle S'}$ mit einer gemeinsamen z-Achse und gemeinsamem Ursprung. Das Koordinatensystem ${\displaystyle S'}$ sei gegenüber ${\displaystyle S}$ um den Winkel ${\displaystyle \varphi }$ um die z-Achse im Uhrzeigersinn gedreht. Ein Punkt P, der im Koordinatensystem S die Koordinaten ${\displaystyle {\vec {x}}=(x,y,z)}$ hat, besitzt dann im Koordinatensystem S' die Koordinaten ${\displaystyle {\vec {x}}'=(x',y',z')}$ mit:

${\displaystyle x'=+x\cos \varphi -y\sin \varphi ,}$

${\displaystyle y'=+x\sin \varphi +y\cos \varphi ,}$

${\displaystyle z'=z.}$

In Matrixschreibweise ergibt sich mit der inversen Drehmatrix für diese Rotation des Koordinatensystems:

${\displaystyle {\vec {x}}'={\begin{pmatrix}\cos \varphi &-\sin \varphi &0\\\sin \varphi &\cos \varphi &0\\0&0&1\end{pmatrix}}{\vec {x}}.}$

Bei der Skalierung werden die „Einheiten“ der Achsen geändert. Das heißt, die Zahlenwerte der Koordinaten ${\displaystyle x_{i}}$ werden mit konstanten Faktoren ${\displaystyle \lambda _{i}}$ multipliziert („skaliert“)

${\displaystyle x_{i}'=\lambda _{i}\cdot x_{i}.}$

Die Parameter dieser Transformation sind die ${\displaystyle N}$ Zahlen ${\displaystyle \lambda _{i}}$. Ein Spezialfall ist die „Maßstabsänderung“, bei der alle Faktoren den gleichen Wert haben

${\displaystyle \lambda _{i}=\lambda .}$

Die Matrix ${\displaystyle A}$ ist in diesem Fall das ${\displaystyle \lambda }$-fache der Einheitsmatrix.

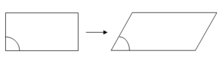
Bei der Scherung verändert sich der Winkel zwischen den Koordinatenachsen. In zwei Dimensionen gibt es daher einen Parameter, im dreidimensionalen Raum drei Parameter.

Affine Transformationen bestehen aus einer linearen Transformation und einer Translation.

Sind beide beteiligten Koordinatensysteme linear, (d. h. im Prinzip durch einen Koordinatenursprung und gleichmäßig unterteilte Koordinatenachsen gegeben), so liegt eine affine Transformation vor. Hierbei sind die neuen Koordinaten affine Funktionen der ursprünglichen, also

${\displaystyle x'_{1}=a_{11}x_{1}+a_{12}x_{2}+\dots +a_{1n}x_{n}+b_{1}}$

${\displaystyle x'_{2}=a_{21}x_{1}+a_{22}x_{2}+\dots +a_{2n}x_{n}+b_{2}}$

${\displaystyle \ldots }$

${\displaystyle x'_{n}=a_{n1}x_{1}+a_{n2}x_{2}+\dots +a_{nn}x_{n}+b_{n}}$

Dies kann man kompakt als Matrixmultiplikation des alten Koordinatenvektors ${\displaystyle {\vec {x}}=(x_{1},\dots ,x_{n})}$ mit der Matrix ${\displaystyle A}$, die die Koeffizienten ${\displaystyle a_{ij}}$ enthält, und Addition eines Vektors ${\displaystyle {\vec {b}}}$, der die ${\displaystyle b_{i}}$ enthält, darstellen

${\displaystyle {\vec {x}}\,'=A{\vec {x}}+{\vec {b}}}$

Die Translation ist ein Spezialfall einer affinen Transformation, bei der A die Einheitsmatrix ist.

Betrachtet werden zwei Koordinatensysteme ${\displaystyle S}$ und ${\displaystyle S'}$. Das System ${\displaystyle S'}$ ist gegenüber ${\displaystyle S}$ um den Vektor ${\displaystyle {\vec {b}}}$ verschoben. Ein Punkt ${\displaystyle P}$, der im Koordinatensystem ${\displaystyle S}$ die Koordinaten ${\displaystyle {\vec {x}}}$ hat, besitzt dann im Koordinatensystem ${\displaystyle S'}$ die Koordinaten ${\displaystyle {\vec {x}}'={\vec {x}}-{\vec {b}}}$.

Ein Punkt in der Ebene wird im kartesischen Koordinatensystem durch seine Koordinaten (x,y) und im Polarkoordinatensystem durch den Abstand ${\displaystyle r}$ vom Ursprung und dem (positiven) Winkel ${\displaystyle {}\varphi }$ zur x-Achse bestimmt.

Dabei gilt für die Umrechnung von Polarkoordinaten in kartesische Koordinaten:

• ${\displaystyle x=r\cdot \cos \varphi }$
• ${\displaystyle y=r\cdot \sin \varphi }$

Für die Umrechnung von kartesischen Koordinaten in Polarkoordinaten gilt:

• ${\displaystyle r={\sqrt {x^{2}+y^{2}}}}$
• ${\displaystyle \varphi ={\begin{cases}\arctan {\frac {y}{x}}&\mathrm {f{\ddot {u}}r} \ x>0\\\arctan {\frac {y}{x}}+\pi &\mathrm {f{\ddot {u}}r} \ x<0,\,y\geq 0\\\arctan {\frac {y}{x}}-\pi &\mathrm {f{\ddot {u}}r} \ x<0,\,y<0\\\pi /2&\mathrm {f{\ddot {u}}r} \ x=0,\,y>0\\-\pi /2&\mathrm {f{\ddot {u}}r} \ x=0,\,y<0\end{cases}}}$

${\displaystyle {}={\begin{cases}\arccos {\frac {x}{r}}&\mathrm {f{\ddot {u}}r} \ y\geq 0\\-\arccos \left({\frac {x}{r}}\right)&\mathrm {f{\ddot {u}}r} \ y<0\end{cases}}}$

Bei der Implementierung der Variante mit ${\displaystyle arccos}$ ist mit Rundungsfehlern zu rechnen, welche bei Nutzung des ${\displaystyle arctan}$ deutlich geringer ausfallen.

In der Physik spielt die Invarianz gewisser Naturgesetze unter Koordinatentransformationen eine besondere Rolle, siehe hierzu Symmetrietransformation. Von besonders grundlegender Bedeutung sind die Galilei-Transformation, Lorentz-Transformation und die Eichtransformation. Häufig gebraucht werden auch Transformationen von Operatoren und Vektoren:

• Die Transformation von Differential-Operatoren
• Die Transformation von Vektorfeldern

In den Geowissenschaften – insbesondere der Geodäsie und Kartografie gibt es noch weitere Transformationen, die formal Koordinatentransformationen darstellen.

• Transformation von geographischer Breite und Länge in Gauß-Krüger-Koordinaten
• Die Umrechnungen zwischen astronomischen Koordinaten
• 7-Parameter-Transformation (Verschiebung, Drehung, Maßstab zwischen zwei Koordinatensystemen auf demselben oder anderen Referenzellipsoid(en), auch Helmert-Transformation („Dreh-Streckung“)).

Im Bereich Robotik gilt die Denavit-Hartenberg-Transformation als das Standardverfahren.

• Liste von Transformationen in der Mathematik
• Substitution (Mathematik)

• I. N. Bronstein, K. A. Semendjajew, G. Musiol: Taschenbuch der Mathematik. 6. vollständig überarbeitete und ergänzte Auflage. Verlag Harry Deutsch, Frankfurt am Main 2005, ISBN 3-8171-2006-0.
• Siegfried Heitz: Koordinaten auf geodätischen Bezugsflächen. Dümmler, Bonn 1985, ISBN 3-427-78981-0.
• Siegfried Heitz: Mechanik fester Körper. Band 1: Grundlagen. Dynamik starrer Körper. Dümmler, Bonn 1980, ISBN 3-427-78921-7.

• WTRANS Software zur Berechnung der Parameter für 2D/3D-Koordinatentransformationen für kartesische und geografische Koordinaten (Molodenski-Ansatz), Projektionen, Geodätische Hauptaufgaben
• MapRef.org, Fachliteratur und Links zu 2D- und 3D-Koordinatentransformationen
• Online-Berechnung von ebenen und räumlichen Koordinatentransformationen mit gegebenen Parametern
• Online-Berechnung von ebenen und räumlichen Koordinatentransformationen aus identischen Punkten (Kontrollpunkten)

1. ↑ Beispielsweise kann die Umwandlung zwischen kartesischen Koordinaten und Kugelkoordinaten nicht durch eine Basiswechselmatrix dargestellt werden. Deshalb ist es zwar eine Koordinatentransformation, aber kein Basiswechsel.
2. ↑ Eric W. Weisstein: Alias Transformation. MathWorld – A Wolfram Web Resource.
3. ↑ Eric W. Weisstein: Alibi Transformation. MathWorld – A Wolfram Web Resource.