Parallel external memory

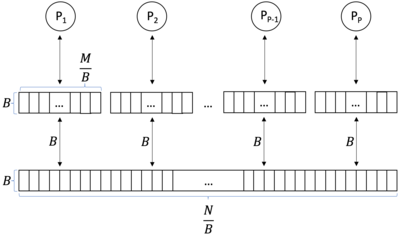
In computer science, a parallel external memory (PEM) model is a cache-aware, external-memory abstract machine.^[1] It is the parallel-computing analogy to the single-processor external memory (EM) model. In a similar way, it is the cache-aware analogy to the parallel random-access machine (PRAM). The PEM model consists of a number of processors, together with their respective private caches and a shared main memory.

Model

Definition

The PEM model^[1] is a combination of the EM model and the PRAM model. The PEM model is a computation model which consists of ${\displaystyle P}$ processors and a two-level memory hierarchy. This memory hierarchy consists of a large external memory (main memory) of size ${\displaystyle N}$ and ${\displaystyle P}$ small internal memories (caches). The processors share the main memory. Each cache is exclusive to a single processor. A processor can't access another’s cache. The caches have a size ${\displaystyle M}$ which is partitioned in blocks of size ${\displaystyle B}$. The processors can only perform operations on data which are in their cache. The data can be transferred between the main memory and the cache in blocks of size ${\displaystyle B}$.

I/O complexity

The complexity measure of the PEM model is the I/O complexity,^[1] which determines the number of parallel blocks transfers between the main memory and the cache. During a parallel block transfer each processor can transfer a block. So if ${\displaystyle P}$ processors load parallelly a data block of size ${\displaystyle B}$ form the main memory into their caches, it is considered as an I/O complexity of ${\displaystyle O(1)}$ not ${\displaystyle O(P)}$. A program in the PEM model should minimize the data transfer between main memory and caches and operate as much as possible on the data in the caches.

Read/write conflicts

In the PEM model, there is no direct communication network between the P processors. The processors have to communicate indirectly over the main memory. If multiple processors try to access the same block in main memory concurrently read/write conflicts^[1] occur. Like in the PRAM model, three different variations of this problem are considered:

• Concurrent Read Concurrent Write (CRCW): The same block in main memory can be read and written by multiple processors concurrently.
• Concurrent Read Exclusive Write (CREW): The same block in main memory can be read by multiple processors concurrently. Only one processor can write to a block at a time.
• Exclusive Read Exclusive Write (EREW): The same block in main memory cannot be read or written by multiple processors concurrently. Only one processor can access a block at a time.

The following two algorithms^[1] solve the CREW and EREW problem if ${\displaystyle P\leq B}$ processors write to the same block simultaneously. A first approach is to serialize the write operations. Only one processor after the other writes to the block. This results in a total of ${\displaystyle P}$ parallel block transfers. A second approach needs ${\displaystyle O(\log(P))}$ parallel block transfers and an additional block for each processor. The main idea is to schedule the write operations in a binary tree fashion and gradually combine the data into a single block. In the first round ${\displaystyle P}$ processors combine their blocks into ${\displaystyle P/2}$ blocks. Then ${\displaystyle P/2}$ processors combine the ${\displaystyle P/2}$ blocks into ${\displaystyle P/4}$. This procedure is continued until all the data is combined in one block.

Comparison to other models

Examples

Multiway partitioning

Let ${\displaystyle M=\{m_{1},...,m_{d-1}\}}$ be a vector of d-1 pivots sorted in increasing order. Let A be an unordered set of N elements. A d-way partition^[1] of A is a set ${\displaystyle \Pi =\{A_{1},...,A_{d}\}}$ , where ${\displaystyle \cup _{i=1}^{d}A_{i}=A}$ and ${\displaystyle A_{i}\cap A_{j}=\emptyset }$ for ${\displaystyle 1\leq i<j\leq d}$. ${\displaystyle A_{i}}$ is called the i-th bucket. The number of elements in ${\displaystyle A_{i}}$ is greater than ${\displaystyle m_{i-1}}$ and smaller than ${\displaystyle m_{i}^{2}}$. In the following algorithm^[1] the input is partitioned into N/P-sized contiguous segments ${\displaystyle S_{1},...,S_{P}}$ in main memory. The processor i primarily works on the segment ${\displaystyle S_{i}}$. The multiway partitioning algorithm (PEM_DIST_SORT^[1]) uses a PEM prefix sum algorithm^[1] to calculate the prefix sum with the optimal ${\displaystyle O\left({\frac {N}{PB}}+\log P\right)}$ I/O complexity. This algorithm simulates an optimal PRAM prefix sum algorithm.

// Compute parallelly a d-way partition on the data segments ${\displaystyle S_{i}}$
for each processor i in parallel do
    Read the vector of pivots M into the cache.
    Partition ${\displaystyle S_{i}}$ into d buckets and let vector ${\displaystyle M_{i}=\{j_{1}^{i},...,j_{d}^{i}\}}$ be the number of items in each bucket.
end for

Run PEM prefix sum on the set of vectors ${\displaystyle \{M_{1},...,M_{P}\}}$ simultaneously.

// Use the prefix sum vector to compute the final partition
for each processor i in parallel do
    Write elements ${\displaystyle S_{i}}$ into memory locations offset appropriately by ${\displaystyle M_{i-1}}$ and ${\displaystyle M_{i}}$.
end for

Using the prefix sums stored in ${\displaystyle M_{P}}$ the last processor P calculates the vector B of bucket sizes and returns it.

If the vector of ${\displaystyle d=O\left({\frac {M}{B}}\right)}$ pivots M and the input set A are located in contiguous memory, then the d-way partitioning problem can be solved in the PEM model with ${\displaystyle O\left({\frac {N}{PB}}+\left\lceil {\frac {d}{B}}\right\rceil >\log(P)+d\log(B)\right)}$ I/O complexity. The content of the final buckets have to be located in contiguous memory.

Selection

The selection problem is about finding the k-th smallest item in an unordered list A of size N. The following code^[1] makes use of PRAMSORT which is a PRAM optimal sorting algorithm which runs in ${\displaystyle O(\log N)}$, and SELECT, which is a cache optimal single-processor selection algorithm.

if ${\displaystyle N\leq P}$ then 
    ${\displaystyle {\texttt {PRAMSORT}}(A,P)}$
    return ${\displaystyle A[k]}$
end if 

//Find median of each ${\displaystyle S_{i}}$
for each processor i in parallel do 
    ${\displaystyle m_{i}={\texttt {SELECT}}(S_{i},{\frac {N}{2P}})}$
end for 

// Sort medians
${\displaystyle {\texttt {PRAMSORT}}(\lbrace m_{1},\dots ,m_{2}\rbrace ,P)}$

// Partition around median of medians
${\displaystyle t={\texttt {PEMPARTITION}}(A,m_{P/2},P)}$

if ${\displaystyle k\leq t}$ then 
    return ${\displaystyle {\texttt {PEMSELECT}}(A[1:t],P,k)}$
else 
    return ${\displaystyle {\texttt {PEMSELECT}}(A[t+1:N],P,k-t)}$
end if

Under the assumption that the input is stored in contiguous memory, PEMSELECT has an I/O complexity of:

${\displaystyle O\left({\frac {N}{PB}}+\log(PB)\cdot \log({\frac {N}{P}})\right)}$

Distribution sort

Distribution sort partitions an input list A of size N into d disjoint buckets of similar size. Every bucket is then sorted recursively and the results are combined into a fully sorted list.

If ${\displaystyle P=1}$ the task is delegated to a cache-optimal single-processor sorting algorithm.

Otherwise the following algorithm^[1] is used:

// Sample ${\displaystyle {\tfrac {4N}{\sqrt {d}}}}$ elements from A
for each processor i in parallel do
    if ${\displaystyle M<|S_{i}|}$ then
        ${\displaystyle d=M/B}$
        Load ${\displaystyle S_{i}}$ in M-sized pages and sort pages individually
    else
        ${\displaystyle d=|S_{i}|}$
        Load and sort ${\displaystyle S_{i}}$ as single page
    end if
    Pick every ${\displaystyle {\sqrt {d}}/4}$'th element from each sorted memory page into contiguous vector ${\displaystyle R^{i}}$ of samples
end for 

in parallel do
    Combine vectors ${\displaystyle R^{1}\dots R^{P}}$ into a single contiguous vector ${\displaystyle {\mathcal {R}}}$
    Make ${\displaystyle {\sqrt {d}}}$ copies of ${\displaystyle {\mathcal {R}}}$: ${\displaystyle {\mathcal {R}}_{1}\dots {\mathcal {R}}_{\sqrt {d}}}$
end do

// Find ${\displaystyle {\sqrt {d}}}$ pivots ${\displaystyle {\mathcal {M}}[j]}$
for ${\displaystyle j=1}$ to ${\displaystyle {\sqrt {d}}}$ in parallel do
    ${\displaystyle {\mathcal {M}}[j]={\texttt {PEMSELECT}}({\mathcal {R}}_{i},{\tfrac {P}{\sqrt {d}}},{\tfrac {j\cdot 4N}{d}})}$
end for

Pack pivots in contiguous array ${\displaystyle {\mathcal {M}}}$

// Partition Aaround pivots into buckets ${\displaystyle {\mathcal {B}}}$
${\displaystyle {\mathcal {B}}={\texttt {PEMMULTIPARTITION}}(A[1:N],{\mathcal {M}},{\sqrt {d}},P)}$

// Recursively sort buckets
for ${\displaystyle j=1}$ to ${\displaystyle {\sqrt {d}}+1}$ in parallel do
    recursively call ${\displaystyle {\texttt {PEMDISTSORT}}}$ on bucket jof size ${\displaystyle {\mathcal {B}}[j]}$
    using ${\displaystyle O\left(\left\lceil {\tfrac {{\mathcal {B}}[j]}{N/P}}\right\rceil \right)}$ processors responsible for elements in bucket j
end for

The I/O complexity of PEMDISTSORT is:

${\displaystyle O\left(\left\lceil {\frac {N}{PB}}\right\rceil \left(\log _{d}P+\log _{M/B}{\frac {N}{PB}}\right)+f(N,P,d)\cdot \log _{d}P\right)}$

where

${\displaystyle f(N,P,d)=O\left(\log {\frac {PB}{\sqrt {d}}}\log {\frac {N}{P}}+\left\lceil {\frac {\sqrt {d}}{B}}\log P+{\sqrt {d}}\log B\right\rceil \right)}$

If the number of processors is chosen that ${\displaystyle f(N,P,d)=O\left(\left\lceil {\tfrac {N}{PB}}\right\rceil \right)}$and ${\displaystyle M<B^{O(1)}}$ the I/O complexity is then:

${\displaystyle O\left({\frac {N}{PB}}\log _{M/B}{\frac {N}{B}}\right)}$

Other PEM algorithms

PEM Algorithm	I/O complexity	Constraints
Mergesort[1]	${\displaystyle O\left({\frac {N}{PB}}\log _{\frac {M}{B}}{\frac {N}{B}}\right)={\textrm {sort}}_{P}(N)}$	${\displaystyle P\leq {\frac {N}{B^{2}}},M=B^{O(1)}}$
List ranking[2]	${\displaystyle O\left({\textrm {sort}}_{P}(N)\right)}$	${\displaystyle P\leq {\frac {N/B^{2}}{\log B\cdot \log ^{O(1)}N}},M=B^{O(1)}}$
Euler tour[2]	${\displaystyle O\left({\textrm {sort}}_{P}(N)\right)}$	${\displaystyle P\leq {\frac {N}{B^{2}}},M=B^{O(1)}}$
Expression tree evaluation[2]	${\displaystyle O\left({\textrm {sort}}_{P}(N)\right)}$	${\displaystyle P\leq {\frac {N}{B^{2}\log B\cdot \log ^{O(1)}N}},M=B^{O(1)}}$
Finding a MST[2]	${\displaystyle O\left({\textrm {sort}}_{P}(|V|)+{\textrm {sort}}_{P}(|E|)\log {\tfrac {|V|}{pB}}\right)}$	${\displaystyle p\leq {\frac {|V|+|E|}{B^{2}\log B\cdot \log ^{O(1)}N}},M=B^{O(1)}}$

Where ${\displaystyle {\textrm {sort}}_{P}(N)}$ is the time it takes to sort N items with P processors in the PEM model.

See also

• Parallel random-access machine (PRAM)
• Random-access machine (RAM)
• External memory (EM)

References