Circuito RC

Un circuito RC es un circuito eléctrico compuesto de resistencias y condensadores. La forma más simple de circuito RC es el circuito RC de primer orden, compuesto por una resistencia y un condensador. Los circuitos RC pueden usarse para filtrar una señal alterna, al bloquear ciertas frecuencias y dejar pasar otras. Los filtros RC más comunes son el filtro paso alto, filtro paso bajo, filtro paso banda, y el filtro de rechazo de banda. Entre las características de los circuitos RC está la de ser sistemas lineales e invariantes en el tiempo.

El circuito RC de la figura se encuentra alimentado por una tensión de entrada Ue. Está en configuración de filtro paso bajo, dado que la tensión de salida del circuito Ua se obtiene en bornes del condensador. Si la tensión de salida fuese la de la resistencia, nos encontraríamos ante una configuración de filtro paso alto.

Este mismo circuito tiene además una utilidad de regulación de tensión, y en tal caso se encuentran configuraciones en paralelo de ambos, la resistencia y el condensador, o alternativamente, como limitador de subidas y bajas bruscas de tensión con una configuración de ambos componentes en serie. Un ejemplo de esto es el circuito Snubber.

Comportamiento en el dominio del tiempo

Carga

El sistema reaccionará de distinta manera de acuerdo a las excitaciones entrantes, como ejemplo, podemos representar la respuesta a la función escalón o la función de salto. La tensión originalmente desde el tiempo 0 subirá hasta que tenga la misma que la fuente, es decir, ${\displaystyle U_{\rm {max}}}$. La corriente entrará en el condensador hasta que entre las placas ya no puedan almacenar más carga por estar en equilibrio electrostático (es decir que tengan la misma tensión que la fuente). De esta forma una placa quedará con carga positiva y la otra con carga negativa, pues esta última tendrá un exceso de electrones.

El tiempo de carga del circuito es proporcional a la magnitud de la resistencia eléctrica R y la capacidad C del condensador. El producto de la resistencia por la capacidad se llama constante de tiempo del circuito (${\displaystyle \tau }$) y tiene un papel muy importante en el comportamiento de este.

${\displaystyle \tau =R\cdot C\,}$

Teóricamente este proceso es infinitamente largo, hasta que U(t)=U_max. En la práctica se considera que el tiempo de carga t_L se mide cuando el condensador se encuentra aproximadamente en la tensión a cargar (más del 99% de ésta), es decir, aproximadamente 5 veces su constante de tiempo.

${\displaystyle t_{L}=5\cdot \tau \,}$

La constante de tiempo ${\displaystyle \tau }$ marca el tiempo en el que la curva tangente en el inicio de la carga marca en intersección con la línea de máxima tensión. Este tiempo sería el tiempo en el que el condensador alcanzaría su tensión máxima si es que la corriente entrante fuera constante. En la realidad, la corriente con una fuente de tensión constante tendrá un carácter exponencial inverso (1/e^kt), igual que la tensión en el condensador.

La máxima corriente ${\displaystyle I_{\rm {max}}}$ fluye cuando el tiempo es inicial (es decir t=0). Esto es debido que el condensador está descargado, y la corriente que fluye se calcula fácilmente a través de la ley de Ohm, con:

${\displaystyle I_{\rm {max}}={\frac {U_{\rm {max}}}{R}}\,}$

Respuesta natural

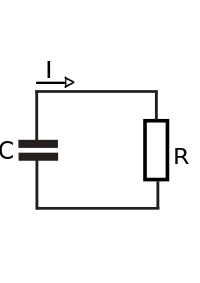
El circuito RC más simple que existe consiste en un condensador y una resistencia en serie. Cuando un circuito consiste solo de un condensador cargado y una resistencia, el condensador descargará su energía almacenada a través de la resistencia. La tensión o diferencia de potencial eléctrico a través del condensador, que depende del tiempo, puede hallarse utilizando la ley de Kirchhoff de corriente, donde la corriente a través del condensador debe ser igual a la corriente a través de la resistencia. Esto resulta en la ecuación diferencial lineal:

${\displaystyle C{\frac {dV}{dt}}+{\frac {V}{R}}=0}$.

Resolviendo esta ecuación para V se obtiene la fórmula de decaimiento exponencial:

${\displaystyle V(t)=V_{0}e^{-{\frac {t}{RC}}}\ ,}$

donde V₀ es la tensión o diferencia de potencial eléctrico entre las placas del condensador en el tiempo t = 0.

El tiempo requerido para que el voltaje caiga hasta ${\displaystyle {\frac {V_{0}}{e}}}$ es denominado "constante de tiempo RC" y es dado por

${\displaystyle \tau =RC\ }$

Impedancia

La impedancia, Z_C (en ohmios) de un condensador con capacidad C (en faradios) es

${\displaystyle Z_{C}={\frac {1}{sC}}}$

La frecuencia compleja s es, en general, un número complejo,

${\displaystyle s\ =\ \sigma +j\omega }$

donde

• j representa la unidad imaginaria:

${\displaystyle j^{2}=-1}$

• ${\displaystyle \sigma \ }$ es el decrecimiento exponencial constante (en radianes por segundo), y
• ${\displaystyle \omega \ }$ es la frecuencia angular sinusoidal (también en radianes por segundo).

Circuito en serie

Viendo el circuito como divisor de tensión, el voltaje a través del condensador es:

${\displaystyle V_{C}(s)={\frac {1/Cs}{R+1/Cs}}V_{in}(s)={\frac {1}{1+RCs}}V_{in}(s)}$

y el voltaje a través de la resistencia es:

${\displaystyle V_{R}(s)={\frac {R}{R+1/Cs}}V_{in}(s)={\frac {RCs}{1+RCs}}V_{in}(s)}$.

Funciones de transferencia

La función de transferencia desde el voltaje de entrada al voltaje a través del condensador es

${\displaystyle H_{C}(s)={V_{C}(s) \over V_{in}(s)}={1 \over 1+RCs}}$.

De forma similar, la función de transferencia desde el voltaje de entrada al voltaje de la resistencia es

${\displaystyle H_{R}(s)={V_{R}(s) \over V_{in}(s)}={RCs \over 1+RCs}}$.

Polos y ceros

Ambas funciones de transferencia tienen un único polo localizado en

${\displaystyle s=-{1 \over RC}}$ .

Además, la función de transferencia de la resistencia tiene un cero localizado en el origen.

Ganancia y fase

La magnitud de las ganancias a través de los dos componentes son:

${\displaystyle G_{C}=|H_{C}(j\omega )|=\left|{\frac {V_{C}(j\omega )}{V_{in}(j\omega )}}\right|={\frac {1}{\sqrt {1+\left(\omega RC\right)^{2}}}}}$

y

${\displaystyle G_{R}=|H_{R}(j\omega )|=\left|{\frac {V_{R}(j\omega )}{V_{in}(j\omega )}}\right|={\frac {\omega RC}{\sqrt {1+\left(\omega RC\right)^{2}}}}}$,

y los ángulos de fase son:

${\displaystyle \phi _{C}=\angle H_{C}(j\omega )=\tan ^{-1}\left(-\omega RC\right)}$

y

${\displaystyle \phi _{R}=\angle H_{R}(j\omega )=\tan ^{-1}\left({\frac {1}{\omega RC}}\right)}$.

Estas expresiones conjuntamente pueden ser sustituidas en la usual expresión para la representación por fasores:

${\displaystyle V_{C}\ =\ G_{C}V_{in}e^{j\phi _{C}}}$

${\displaystyle V_{R}\ =\ G_{R}V_{in}e^{j\phi _{R}}}$.

Corriente

La corriente en el circuito es la misma en todos los puntos del circuito ya que el circuito está en serie:

${\displaystyle I(s)={\frac {V_{in}(s)}{R+{\frac {1}{Cs}}}}={Cs \over 1+RCs}V_{in}(s)}$

Respuesta a impulso

La respuesta a impulso para cada voltaje es la inversa de la transformada de Laplace de la correspondiente función de transferencia. Esta representa la respuesta del circuito a una entrada de voltaje consistente en un impulso o función delta de Dirac.

La respuesta impulso para el voltaje del condensador es

${\displaystyle h_{C}(t)={1 \over RC}e^{-t/RC}u(t)={1 \over \tau }e^{-t/\tau }u(t)}$

donde u(t) es la función escalón de Heaviside y

${\displaystyle \tau \ =\ RC}$

es la constante de tiempo.

De forma similar, la respuesta impulso para el voltaje de la resistencia es

${\displaystyle h_{R}(t)=\delta (t)-{1 \over RC}e^{-t/RC}u(t)=\delta (t)-{1 \over \tau }e^{-t/\tau }u(t)}$

donde δ(t) es la función delta de Dirac

Análisis de frecuencia

Un análisis de frecuencia del montaje permite determinar cuáles son las frecuencias que el filtro rechaza y cuáles las que acepta. Para bajas frecuencias, ${\displaystyle H_{C}}$ tiene un módulo cercano a 1 y una fase próxima a 0. Cuando la frecuencia aumenta, su módulo disminuye para tender a 0 mientras que la fase tiende a ${\displaystyle -\pi /2}$. Por el contrario, ${\displaystyle H_{R}}$ posee un módulo cercano a 0 a bajas frecuencias y una fase próxima a ${\displaystyle \pi /2}$ y cuando la frecuencia aumenta, el módulo tiende a 1 y su fase tiende a 0.

Cuando ${\displaystyle \omega \to 0}$ :

${\displaystyle G_{C}\to 1}$ y ${\displaystyle \varphi _{C}\to 0}$.

${\displaystyle G_{R}\to 0}$ y ${\displaystyle \varphi _{R}\to 90^{\circ }=\pi /2}$.

Cuando ${\displaystyle \omega \to \infty }$ :

${\displaystyle G_{C}\to 0}$ y ${\displaystyle \varphi _{C}\to -90^{\circ }=-\pi /2}$

${\displaystyle G_{R}\to 1}$ y ${\displaystyle \varphi _{R}\to 0}$.

Así, cuando la salida del filtro está tomada sobre el condensador el comportamiento es de tipo filtro paso bajo: las altas frecuencias son atenuadas y las bajas frecuencias pasan. Si la salida está tomada sobre la resistencia, se produce el proceso inverso y el circuito se comporta como un filtro paso alto.

La frecuencia de corte ${\displaystyle f_{c}}$ del circuito que define el límite tiene 3 dB entre las frecuencias atenuadas y aquellas que no lo son; es igual a:

${\displaystyle f_{c}={\frac {1}{2\pi RC}}}$ (en Hz)

Análisis temporal

Por razones de simplicidad, el análisis temporal se efectuará utilizando la transformada de Laplace p. Suponiendo que el circuito está sometido a una escalón de tensión de amplitud V de entrada ( ${\displaystyle V_{in}=0\,}$ para ${\displaystyle t=0\,}$ y ${\displaystyle V_{in}=V\,}$ sinon) :

${\displaystyle V_{in}(p)={\frac {V}{p}}}$

${\displaystyle V_{C}(p)=H_{C}(p)V_{in}(p)={\frac {1}{1+pRC}}{\frac {V}{p}}}$

${\displaystyle V_{R}(p)=H_{R}(p)V_{in}(p)={\frac {pRC}{1+pRC}}{\frac {V}{p}}}$.

La transformada de Laplace inversa de estas expresiones resulta:

${\displaystyle V_{C}(t)=V\left(1-e^{-t/RC}\right)}$

${\displaystyle V_{R}(t)=Ve^{-t/RC}\,}$.

En este caso, el condensador se carga y la tensión en los bornes tiende a V, mientras que en los bornes de la resistencia tiende a 0.

El circuito RC posee una constante de tiempo, generalmente expresado como ${\displaystyle \tau =RC\,}$, que representa el tiempo que toma la tensión para efectuar el 63% (${\displaystyle 1-e^{-1}}$) de la variación necesaria para pasar del valor inicial al final.

Igualmente es posible derivar estas expresiones de las ecuaciones diferenciales que describen el circuito:

${\displaystyle {\frac {V_{in}-V_{C}}{R}}=C{\frac {dV_{C}}{dt}}}$

${\displaystyle V_{R}=V_{in}-V_{C}\,}$.

Las soluciones son exactamente las mismas que aquellas obtenidas mediante la transformada de Laplace.

Integrador

A alta frecuencia, es decir cuando ${\displaystyle \omega >>{\frac {1}{RC}}}$, el condensador no tiene tiempo suficiente para cargarse y la tensión en los bornes permanece pequeña.

Así:

${\displaystyle V_{R}\approx V_{in}}$

y la intensidad en el circuito vale por tanto:

${\displaystyle I\approx {\frac {V_{in}}{R}}}$.

Como,

${\displaystyle V_{C}={\frac {1}{C}}\int _{0}^{t}Idt}$

se obtiene:

${\displaystyle V_{C}\approx {\frac {1}{RC}}\int _{0}^{t}V_{in}dt}$ .

La tensión en los bornes del condensador integrado se comporta como un filtro de paso-bajo.

Derivador

A baja frecuencia, es decir cuando ${\displaystyle \omega <<{\frac {1}{RC}}}$, el condensador tiene el tiempo de cargarse casi completamente.

Entonces,

${\displaystyle I\approx {\frac {V_{in}}{1/j\omega C}}}$

${\displaystyle V_{in}\approx {\frac {I}{j\omega C}}\approx V_{C}}$

Ahora,

${\displaystyle V_{R}=IR=C{\frac {dV_{C}}{dt}}R}$

${\displaystyle V_{R}\approx RC{\frac {dV_{in}}{dt}}}$.

La tensión en los bornes de la resistencia derivado se comporta como un filtro de paso-alto.

Circuito en paralelo

El circuito RC en paralelo generalmente es de menor interés que el circuito en serie. Esto es en gran parte debido a que la tensión de salida ${\displaystyle V_{out}}$ es igual a la tensión de entrada ${\displaystyle V_{in}}$ — como resultado, el circuito no actúa como filtro de la señal de entrada si no es alimentado por una fuente de corriente.

Con impedancias complejas:

${\displaystyle I_{R}={\frac {V_{in}}{R}}\,}$

y

${\displaystyle I_{C}=j\omega CV_{in}\,}$.

Esto muestra que la corriente en el condensador está desfasada 90° de fase con la resistencia (y la fuente de corriente). Alternativamente, las ecuaciones diferenciales de gobierno que pueden usarse son:

${\displaystyle I_{R}={\frac {V_{in}}{R}}}$

y

${\displaystyle I_{C}=C{\frac {dV_{in}}{dt}}}$.

Cuando es alimentado por una fuente de corriente, la función de transferencia de un circuito RC en paralelo es:

${\displaystyle {\frac {V_{out}}{I_{in}}}={\frac {R}{1+sRC}}}$.

Véase también

• Circuito RL

• Circuito LC
• Circuito RLC
• Circuito

Enlaces externos

• RC-Glied Berechnung Übergangsfrequenz und Zeitkonstante