Espiral sinusoidal

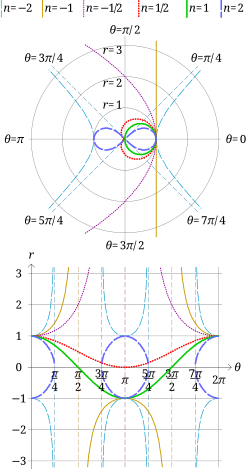
En geometría, las espirales sinusoidales son una familia de curvas definidas por la ecuación en coordenadas polares

${\displaystyle r^{n}=a^{n}\cos(n\theta )\,}$

donde a es una constante distinta de cero y n es un número racional distinto de cero. Con una rotación sobre el origen, la ecuación también se puede escribir como

${\displaystyle r^{n}=a^{n}\sin(n\theta ).\,}$

El término "espiral" es un nombre inapropiado, porque en realidad no son espirales, y a menudo tienen forma lobulada. Muchas curvas bien conocidas son espirales sinusoidales, entre las que se incluyen:

• Hipérbola equilátera (n = −2)
• Recta (n = −1)
• Parábola (n = −1/2)
• Cúbica de Tschirnhausen (n = −1/3)
• Sexteto de Cayley (n = 1/3)
• Cardioide (n = 1/2)
• Circunferencia (n = 1)
• Lemniscata de Bernoulli (n = 2)

Las curvas fueron estudiadas por primera vez por Colin Maclaurin.

Ecuaciones

Diferenciando

${\displaystyle r^{n}=a^{n}\cos(n\theta )\,}$

y eliminando a, resulta una ecuación diferencial para r y θ:

${\displaystyle {\frac {dr}{d\theta }}\cos n\theta +r\sin n\theta =0}$.

Entonces

${\displaystyle \left({\frac {dr}{ds}},\ r{\frac {d\theta }{ds}}\right)\cos n\theta {\frac {ds}{d\theta }}=\left(-r\sin n\theta ,\ r\cos n\theta \right)=r\left(-\sin n\theta ,\ \cos n\theta \right)}$

lo que implica que el ángulo tangencial polar es

${\displaystyle \psi =n\theta \pm \pi /2}$

y entonces el ángulo tangencial es

${\displaystyle \varphi =(n+1)\theta \pm \pi /2}$.

(El signo aquí es positivo si r y cos nθ tienen el mismo signo, y negativo de lo contrario).

El vector tangente unidad,

${\displaystyle \left({\frac {dr}{ds}},\ r{\frac {d\theta }{ds}}\right)}$,

tiene longitud uno, por lo que la comparación de la magnitud de los vectores en cada lado de la ecuación anterior da

${\displaystyle {\frac {ds}{d\theta }}=r\cos ^{-1}n\theta =a\cos ^{-1+{\tfrac {1}{n}}}n\theta }$.

En particular, la longitud de un solo bucle cuando ${\displaystyle n>0}$ es:

${\displaystyle a\int _{-{\tfrac {\pi }{2n}}}^{\tfrac {\pi }{2n}}\cos ^{-1+{\tfrac {1}{n}}}n\theta \ d\theta }$

La curvatura viene dada por

${\displaystyle {\frac {d\varphi }{ds}}=(n+1){\frac {d\theta }{ds}}={\frac {n+1}{a}}\cos ^{1-{\tfrac {1}{n}}}n\theta }$.

Propiedades

La curva inversa de una espiral sinusoidal con respecto a un círculo con centro en el origen es otra espiral sinusoidal cuyo valor de n es el negativo del valor de la curva original de parámetro n. Por ejemplo, el inverso de la lemniscata de Bernoulli es una hipérbola.

La isóptica, la podaria y la podal negativa de una espiral sinusoidal son diferentes espirales sinusoidales.

Un camino de una partícula que se mueve de acuerdo con un fuerza central proporcional a una potencia de r es una espiral sinusoidal.

Cuando n es un número entero, y n puntos se distribuyen regularmente en un círculo de radio a, entonces el conjunto de puntos de modo que la media geométrica de las distancias desde el punto al n puntos es una espiral sinusoidal. En este caso, la espiral sinusoidal es una lemniscata polinomial.

Referencias

• Yates, R. C .: Un manual sobre curvas y sus propiedades , J. W. Edwards (1952), "Spiral" p. 213 & ndash; 214
• "Espiral sinusoidal" en www.2dcurves.com
• "Espirales sinusoidales" en The MacTutor History of Mathematics Archivado el 7 de abril de 2012 en Wayback Machine.
• Weisstein, Eric W. «Sinusoidal Spiral». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 

Enlaces externos

• Wikimedia Commons alberga una categoría multimedia sobre Espiral sinusoidal.