Integral de Riemann

En la rama de las matemáticas conocida como análisis real, la integral de Riemann, creada por Bernhard Riemann en un artículo publicado en 1854, fue la primera definición rigurosa de la integral de una función en un intervalo.^[1]​ Para muchas funciones y aplicaciones prácticas, la integral de Riemann puede ser evaluada utilizando el teorema fundamental del cálculo o aproximada mediante integración numérica.

La integral de Riemann es inadecuada para muchos propósitos teóricos. Algunas de las deficiencias técnicas en la integración de Riemann se pueden remediar con la integral de Riemann-Stieltjes, y la mayoría desaparecen con la integral de Lebesgue.

La integral de Riemann de una función real de variable real se denota usualmente de la siguiente forma:

${\displaystyle \int _{a}^{b}f(x)\;dx}$

Si bien el artículo en gran parte se restringe a la integración sobre intervalos acotados de ${\displaystyle [a,b]\subset \mathbb {R} ^{1}}$, el concepto puede generalizarse a dominios acotados de ${\displaystyle \mathbb {R} ^{n}}$ sin mucha dificultad.

Marco general

Sean ${\displaystyle f:[a,b]\to \mathbb {R} }$ una función no negativa y

${\displaystyle S=\{(x,y)\in \mathbb {R} :a\leq x\leq b,0\leq y\leq f(x)\}}$

la región en el plano bajo la gráfica de la función ${\displaystyle f}$ y por encima del intervalo ${\displaystyle [a,b]}$. Estamos interesados en medir el área de ${\displaystyle S}$, una vez que ya la hemos medido, denotaremos el área por

${\displaystyle \int _{a}^{b}f(x)\;dx}$

La idea básica de la integral de Riemann es utilizar aproximaciones para calcular el área de ${\displaystyle S}$. Tomando mejores aproximaciones, podremos decir que “en el límite” tendremos exactamente el área de ${\displaystyle S}$ bajo la curva.

Definición

Se van a definir cuatro conceptos, el último siendo el que nos interesa: el primero una partición de un intervalo ${\displaystyle [a,b]}$, el segundo la norma de una partición, el tercero una suma de Riemann y el último que una función acotada sea Riemann integrable en un intervalo ${\displaystyle [a,b]}$.

Partición de un intervalo y su norma

Sea ${\displaystyle [a,b]}$ un intervalo cerrado sobre los números reales, una partición de ${\displaystyle [a,b]}$ es un subconjunto finito ${\displaystyle P=\{x_{0}=a,\;x_{1},\;\dots ,\;x_{n}=b\}}$ tal que ${\displaystyle x_{i}>x_{i-1}}$, con ${\displaystyle i=1,\dots ,n}$. La norma de la partición es la longitud del intervalo más grande:

${\displaystyle \|P\|=\max \left\lbrace x_{i}-x_{i-1}:i=1,...,n\right\rbrace }$

Lo que estamos haciendo, en pocas palabras, es cortar al intervalo en subintervalos disjuntos, cuya unión forma el intervalo original. La norma es la longitud del intervalo más grande.

Suma de Riemann

Sea ${\displaystyle f:[a,b]\to \mathbb {R} }$ una función y tomemos una partición del intervalo ${\displaystyle [a,b]}$, denotada por ${\displaystyle P=\{x_{0}=a,\;x_{1},\;\dots ,\;x_{n}=b\}}$, entonces llamamos suma de Riemann a una suma de la forma:

${\displaystyle \sum _{k=1}^{n}f(t_{k})(x_{k}-x_{k-1})}$

con ${\displaystyle x_{k-1}\leq t_{k}\leq x_{k}}$.

De manera intuitiva esta suma representa la suma de áreas de rectángulos con base ${\displaystyle x_{k}-x_{k-1}}$ y altura ${\displaystyle f(t_{k})}$. Simbolizamos esta suma como ${\displaystyle S(P,f)}$, también se utiliza la notación más extensa pero más explícita:

${\displaystyle S(P,f,\left\lbrace t_{i}\right\rbrace _{i=1}^{n})}$

Integrabilidad de Riemann

Una función ${\displaystyle f}$ acotada definida en un intervalo ${\displaystyle [a,b]}$ se dice que es Riemann integrable en ${\displaystyle [a,b]}$ si existe un número ${\displaystyle I}$ en los reales tal que, para todo número real positivo ${\displaystyle \varepsilon }$ existe una ${\displaystyle \delta }$ positiva tal que si ${\displaystyle P}$ es una partición de ${\displaystyle [a,b]}$ con ${\displaystyle \|P\|<\delta }$ y ${\displaystyle S(P,f)}$ es cualquier suma de Riemann entonces ${\displaystyle |S(P,f)-I|<\varepsilon }$.

Usualmente para funciones conocidas que sabemos integrables se toma una partición regular del intervalo y se toman los ${\displaystyle t_{k}}$ como alguno de los puntos extremos de cada intervalo. Notar que si no supiéramos que la función es integrable entonces no podríamos tomar cualquier punto del intervalo arbitrariamente, es decir, no podríamos tomar los valores extremos. En este caso en que no sabemos que es integrable, tendríamos que revisar que para cualquier valor ${\displaystyle t_{k}}$ que tomáramos en cada intervalo ${\displaystyle [x_{k-1},x_{k}]}$ la suma de Riemann menos algún número real ${\displaystyle I}$ es menor en valor absoluto que cualquier ${\displaystyle \varepsilon }$ que hubiéramos tomado. En caso de cumplirse habríamos demostrado que la función f es integrable según Riemann en ${\displaystyle [a,b]}$ y habríamos hallado su valor; en caso de no cumplirse no habríamos probado nada en absoluto. Cuando llevamos al límite esta partición, se puede demostrar que obtenemos el valor de la integral:

${\displaystyle \int _{a}^{b}f(x)\;dx=\lim _{n\to \infty }{\frac {b-a}{n}}\sum _{k=1}^{n}f\left(a+k\;{\frac {b-a}{n}}\right)}$.

Esta última expresión es sobre todo útil para funciones que sabemos que son integrables como, por ejemplo, las continuas. Podemos demostrar que toda función que es continua en un intervalo ${\displaystyle [a,b]}$, es integrable, en cuyo caso lo único que restaría sería encontrar el valor de la integral. Por supuesto, si ya estamos familiarizados con el Segundo Teorema Fundamental del Cálculo entonces basta hallar una función ${\displaystyle F(x)}$ (denominada primitiva de ${\displaystyle f(x)}$) cuya derivada nos dé nuestra función original ${\displaystyle f(x)}$ y entonces el valor de la integral es ${\displaystyle F(b)-F(a)}$. No siempre podemos hallar una función primitiva de la que estamos integrando. En esos casos, se recurre a una expresión como la anterior o a métodos de aproximación.

Condición necesaria y suficiente para la integrabilidad de Riemann

En este apartado nos referiremos a funciones acotadas en un intervalo cerrado ${\displaystyle [a,b]}$ (igual que en los apartados anteriores).

Una función no ha de ser continua para ser integrable de Riemann (no obstante esta es una condición suficiente); de hecho una función continua en todo el intervalo salvo en un punto es integrable de Riemann, incluso una función con un número numerable de discontinuidades es integrable y en el caso extremo ciertas funciones con un número no numerable de discontinuidades pueden ser integrables. El siguiente teorema establece que una función es integrable si y solo si su conjunto de discontinuidades se puede recubrir por conjuntos abiertos tales que la suma de sus anchuras puede hacerse arbitrariamente pequeña.

Criterio de Lebesgue para la integrabilidad de Riemann Sea ${\displaystyle f}$ una función definida y acotada en ${\displaystyle [a,b]}$ y sea ${\displaystyle D}$ el conjunto de las discontinuidades de ${\displaystyle f}$ en ${\displaystyle [a,b]}$. Entonces ${\displaystyle f\in R}$ (con ${\displaystyle R}$ el conjunto de las funciones Riemann integrables) en ${\displaystyle [a,b]}$ si, y solo si, ${\displaystyle D}$ tiene medida cero.

De este modo, cualquier función continua o con un conjunto numerable de discontinuidades es integrable. Como ejemplo de función con un conjunto no numerable de discontinuidades e integrable tenemos por ejemplo:

${\displaystyle f(x)={\begin{cases}1,&{\mbox{si }}x\in C\\0,&{\mbox{si }}x\notin C\end{cases}}}$

siendo C el conjunto de Cantor.

Definiciones equivalentes

Existen definiciones que son equivalentes a la definición de integral de Riemann. Son equivalentes en el sentido de que podemos demostrar que una función es integrable respecto a una cierta definición si y solo si es integrable con respecto a otra definición. Una muy utilizada es la integral de Darboux que se auxilia de los supremos e ínfimos de los intervalos en los cuales se particiona. Una segunda, que es la que de hecho se utiliza para definir la integral de Riemann-Stieltjes, con los ajustes necesarios (y no la definición que se encuentra arriba, porque cuando se extiende a ser de Riemann-Stieltjes no cumple con todo lo que nos gustaría que se pudiera derivar de dicha definición) es la siguiente:

Una función ${\displaystyle f}$ acotada definida en un intervalo ${\displaystyle [a,b]}$ se dice que es Riemann integrable en ${\displaystyle [a,b]}$ si existe un número ${\displaystyle I}$ tal que, para todo número real positivo ${\displaystyle \varepsilon }$ existe una partición ${\displaystyle P\varepsilon }$ de ${\displaystyle [a,b]}$ tal que si ${\displaystyle P}$ es un refinamiento de ${\displaystyle P\varepsilon }$ (es decir, ${\displaystyle P}$ contiene a ${\displaystyle P\varepsilon }$) y ${\displaystyle S(P,f)}$ es cualquier suma de Riemann, entonces ${\displaystyle |S(P,f)-I|<\varepsilon }$.

De manera intuitiva, la diferencia entre la definición de la integral de Riemann y esta última definición, es que la primera hace uso del concepto de la norma de la partición menor que un cierto delta para obtener mejores aproximaciones, en la segunda por contraste nos olvidamos de la norma de la partición y en vez de eso ampliamos las particiones, es decir les añadimos puntos, para obtener mejores aproximaciones. Esta diferencia es muy importante para el concepto de la integral de Riemann-Stieltjes, porque en la segunda definición nosotros podemos decir específicamente qué puntos queremos incluir en la partición, en contraste a la primera, en la que estamos atados a una cierta norma, que aunque se cumpla que la norma sea menor que un cierto delta, puede ser que la partición no incluya puntos que queremos que incluya en específico (que en el caso de la integral de Riemann no nos importa, pero cuando utilizamos la integral de Riemann-Stieltjes, hay puntos que son críticos para que se cumplan ciertas propiedades).

Notación y otras integrales

El símbolo ${\textstyle \int }$ es una «S» deformada. En el caso en que la función ${\displaystyle f}$ tenga varias variables, el ${\displaystyle dx}$ especifica la variable de integración.
Si la variable de integración y el intervalo de integración son conocidos, la notación se puede simplificar como ${\textstyle \int f}$.

Algunas funciones no son Riemann integrables; tal es el caso de la función de Dirichlet. La integral de Darboux, la integral de Lebesgue, la integral de Riemann-Stieltjes y otras más que se pueden ver en artículo sobre integración son otras formas de atacar el problema de la integración, logrando en algunos casos que funciones que no son Riemann integrables sean por ejemplo Lebesgue integrables.

Históricamente, Riemann concibió esta teoría de integración, y proporcionó algunas ideas para el teorema fundamental del cálculo diferencial e integral. La teoría de la integración de Lebesgue llegó mucho más tarde, cuando los puntos débiles de la integral de Riemann se comprendían mejor.

Interpretación geométrica

En Análisis real, la integral de Riemann es una forma simple de definir la integral de una función sobre un intervalo como el área localizada bajo la curva de la función.

Sea ${\displaystyle f}$ una función con valores reales definida sobre el intervalo ${\displaystyle [a,b]}$, tal que para todo ${\displaystyle x}$, ${\displaystyle f(x)\geq 0}$ (es decir, tal que ${\displaystyle f}$ es no negativa).

Sea ${\displaystyle S_{f}=\{(x,y)|0\leq y\leq f(x)}$ la región del plano delimitada por la curva correspondiente a la función ${\displaystyle f}$, el eje de las abscisas y las rectas verticales de ecuaciones ${\displaystyle x=a}$ y ${\displaystyle x=b}$. Estamos interesados en medir el área del dominio ${\displaystyle S}$, si es que se puede medir.

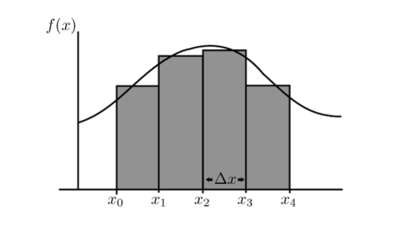
Para obtener una aproximación al área encerrada debajo de una curva, se la puede dividir en rectángulos como indica la figura.

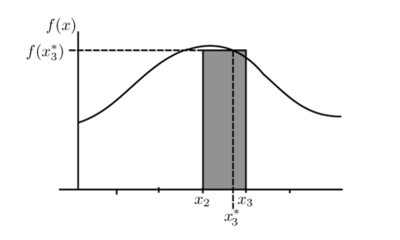
El área de cada rectángulo, es el producto de la función en un punto, por el ancho del intervalo.

Al aumentar el número de rectángulos se obtiene una mejor aproximación.

.

.

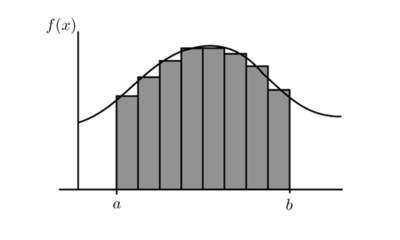Véase también

• Integral de Riemann-Stieltjes
• Integral de Lebesgue
• Integral de Itō (1945)

Referencias

Bibliografía

• APOSTOL, Tom M. Análisis Matemático (Mathematical Analysis), trad., ed. Reverté S. A. 1976.
• APOSTOL, Tom M. Cálculus Volumen 1 y 2(Calculus), trad., ed. Reverté S.A. 1984.
• BARTLE, Robert G. Introducción al Análisis Matemático (The Elements of Real Analysis), trad., ed. Limusa S.A. 1982.
• BARTLE et al. Introducción al Análisis Matemático de una Variable (Introduction to Real Analysis), trad., ed. Limusa S.A. 2009.
• KURTZ et al.Theories of Integration The Integrals of Riemann, Lebesgue, Henstock-Kurzweil and McShane, ed. World Scientific Publishing Co. Pte. Ltd. 2004.
• SPIVAK, Michael. Cálculo Infinitesimal(Calculus), trad., ed. Reverté S.A. 1992.

Enlaces externos

• Integral de Riemann (Departamento de Matemática Aplicada. Facultad de Informática de la Universidad Politécnica de Madrid)
• Integral definida (Manuel Sada Allo): Ejemplo 1 Ejemplo 2