Erlatibitate berezia

Fisikan, erlatibitate berezia deritzo espazioaren eta denboraren portaera azaltzen duen teoria fisikoari. Mekanika newtondarraren orokorpen bat da eta bateragarria da Maxwellen teoria elektromagnetikoarekin.

Albert Einsteinek 1905. urtean argitaratu zuen Zur Elektrodynamik bewegter Körper artikuluan agertzen da lehen aldiz erlatibitate berezia^[1]. Espazioa eta denbora erlatiboak direla iragartzen du, hots, behatzailearen higiduraren araberakoak direla. Besteak beste, denboraren zabalkuntza, espazioaren uzkurdura edota aldiberekotasunaren erlatibitatea aurresaten ditu.

Teoriaren baliagarritasuna grabitazio-eremu ahuletara dago mugatuta. Grabitazio-eremuak oso bortitzak direnean, orokorragoa den erlatibitate orokorra behar dugu espazio-denboraren deskribapen egoki bat egiteko^[2]. Era berean, gorputzen abiadurak txikiak direnean argiaren abiaduraren aldean, ez da beharrezkoa erlatibitate berezia erabiltzea (bai ordea, zuzena), Mekanika Newtondarrak emaitza onargarriak ematen baititu.

Einstein-en postulatuak

Einsteinek, erlatibitate bereziaren teoria, bi postulatu oinarri zituela eraiki zuen, 1905. urtean:

1. Erlatibitatearen printzipioa: fisikaren oinarrizko legeak modu berean azaltzen dira erreferentzia-sistema inertzial guztietan. Fisika berdina da higidura zuzen uniformean doan edo geldirik dagoen behatzailearen ikuspuntutik.
2. Argiaren abiaduraren aldaezintasunaren printzipioa: hutsean, argiaren abiadura ez da behatzailearen eta iturriaren mendekoa^[3]. Hots, abiadura berbera da erreferentzia-sistema guztietan: ${\displaystyle c=3\cdot 10^{8}m/s.}$

Bigarren printzipioa Maxwellen elektrodinamikaren teoriaren ondorioz postulatu zuen^[4]. Izan ere, Maxwellen ekuazioak sistema inertzial guztietan betetzen badira, ${\displaystyle c}$ abiadura sistema inertzialekiko independentea da. Hau da, argiaren abiadura hutsaren ezaugarri unibertsala da, eta ez erreferentzia-sistema berezi batean neurturiko ezaugarria.

Lorentz-en transformazioak

Lorentzen transformazioak, Lorentzen faktorearen bidez, bi behatzailek neurturiko magnitude fisikoak erlazionatzen ditu.

Lorentzen faktorea honako era honetan definitzen da:

${\displaystyle \gamma \equiv {\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}$

Demagun bi behatzaile ditugula, non ${\displaystyle S'}$ sistemako behatzailea ${\displaystyle S}$ sistemako behatzailearekiko ${\displaystyle v}$ abiadura uniformean higitzen den ${\displaystyle x}$ ardatzean. Lorentzen faktorearen bitartez, ${\displaystyle S}$ eta ${\displaystyle S'}$ sistemetako behatzaileek neurtuko dituzten oinarrizko magnitude fisikoak erlaziona daitezke:

${\displaystyle t=\gamma \left(t'+{\frac {v}{c^{2}}}x'\right)}$

${\displaystyle x=\gamma \left(x'+vt'\right)}$

${\displaystyle y=y'}$

${\displaystyle z=z'}$

Alderantzizko transformatuak, berriz, ${\displaystyle v}$ abiadura ${\displaystyle -v}$ abiadurarekin ordezkatuz eta ${\displaystyle \gamma }$ berdin mantenduz lortzen dira:

${\displaystyle t'=\gamma \left(t-{\frac {v}{c^{2}}}x\right)}$

${\displaystyle x'=\gamma \left(x-vt\right)}$

${\displaystyle y'=y}$

${\displaystyle z'=z}$

Funtzioak linealak direnez, denbora- eta espazio-tarteak (${\displaystyle {\ce {\Delta t}}}$, ${\displaystyle \Delta x}$) ere modu berean transformatzen dira:

${\displaystyle \Delta t=\gamma \left(\Delta t'+{\frac {v}{c^{2}}}\Delta x'\right)}$

${\displaystyle \Delta x=\gamma \left(\Delta x'+v\Delta t'\right)}$

${\displaystyle \Delta y=\Delta y'}$

${\displaystyle \Delta z=\Delta z'}$

Alderantzizko transformazioak:

${\displaystyle \Delta t'=\gamma \left(\Delta t-{\frac {v}{c^{2}}}\Delta x\right)}$

${\displaystyle \Delta x'=\gamma \left(\Delta x-v\Delta t\right)}$

${\displaystyle \Delta y'=\Delta y}$

${\displaystyle \Delta z'=\Delta z}$

Ohartu Lorentzen faktorea ia bat bihurtzen dela sistemen arteko abiadura argiarena baino askoz txikiagoa denean:

${\displaystyle {\frac {v}{c}}<<1\ \ \Longrightarrow \ \ \gamma \approx {}1}$

Horrelako kasuetan, adierazi berri ditugun Lorentzen transformazioak Galileoren transformazio bihurtzen dira. Ondorioz, gure egunerokotasunean, sistema makroskopikoan aurkitzen ditugun abiadurak argiarena baino askoz txikiagoak izaten direnez, oso erabilgarriak egiten zaizkigu Galileo eta Newtonen mekanikak. Bestalde, horren ondoriotako bat izan daiteke erlatibitate bereziaren hainbat ondorio ulertzeko zailtasunak izatea, ez baikaude ohituta horrelako fenomenoak behatzera. Abiadura handiko fenomeno horiek aztertu ahal izateko, gure eskala asko aldatu beharra daukagu, mundu makroskopikoan eta astrofisikan eta kosmologian gertatzen baitira soilik zuzenean.

Berebat, bi sistemen arteko abiadura ${\displaystyle |{\vec {v}}|=c}$ denean, Lorentzen koefizientea infinitu bihurtzen da. Ondorioz, beste behin ere ikusten dugu sistemen arteko abiadura ezin dela ${\displaystyle c}$ edo handiagoa izan.

Minkowskiren diagramak

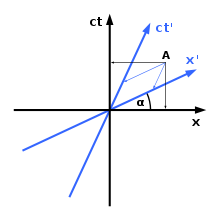
Esan bezala, erlatibitate bereziaren hainbat ondorio oso zailak dira ulertzen. Zailtasun hori errazteko asmoz, Minkowski-ren diagrama erabiltzen dira. Minkowskiren diagramak espazio-denbora deskribatzeko erabiltzen diren ${\displaystyle 4}$ dimentsioko tresna grafikoak dira. Diagrama horiek irudikatzean, gertaerek denbora-osagai bat dutenez, denbora hartzen da ardatzetako batean; besteetan, berriz, espazioaren hiru osagaiak. Ardatz guztien dimentsioak berdinak izan daitezen, denbora-ardatza ${\displaystyle c}$ argiaren abiadurarekin biderkatzen da; horrela, ${\displaystyle ct}$, ${\displaystyle x}$, ${\displaystyle y}$ eta ${\displaystyle z}$ ardatzak lortzen dira.

Minkowskiren diagramen arazoa da paperean ezinezkoa dela elkarzut diren lau ardatz irudikatzea. Aztertzen diren kasurik sinpleenak, ordea, dimentsio batekoak izan ohi dira. Demagun gure gertaera ${\displaystyle x}$ ardatzean soilik jazo dela. Gertaera hori irudikatzeko nahikoa izango da ${\displaystyle ct}$ eta ${\displaystyle x}$ ardatzak soilik irudikatzea, ${\displaystyle y}$ eta ${\displaystyle z}$ ardatzak konstante mantenduko baitira. Erlatibitate berezian, ${\displaystyle ct}$ ardatza beti ardatz bertikalean irudikatzen da. Horrela, ${\displaystyle S}$ eta ${\displaystyle S'}$ sistemen diagramak:

Diagrama horien erabilgarritasuna aztertzeko, demagun ${\displaystyle S}$ sistemarekiko ${\displaystyle v}$ abiaduran higitzen den partikula bat, non ${\displaystyle S'}$ sisteman geldirik mantentzen den (ohartu ${\displaystyle S'}$ sistema ${\displaystyle S}$ sistemarekiko ${\displaystyle v}$ abiaduran higitzen dela). ${\displaystyle S}$ sisteman, partikularen higidura ${\displaystyle x=x_{0}+vt}$ ekuazioak deskribatuko du. Baina, oraingoan denbora ordenatuetan dagonenez, diagraman partikularen eboluzioa

${\displaystyle ct={\frac {c}{v}}(x-x_{0})}$ adierazpenak ematen du. Horrek ${\displaystyle {\frac {c}{v}}}$ maldako lerroa ematen du, eta zuzen horri unibertso-lerroa deitzen zaio. ${\displaystyle S'}$ sisteman berriz, unibertso-lerroa, ${\displaystyle x'=x_{0}'}$lerro zuzen bertikala izango da.

Aipatzekoa da, baita ere, Minkowskiren diagramen bitartez Einsteinen bigarren printzipioa modu grafikoan froga daitekeela. Demagun ${\displaystyle OX}$ eta ${\displaystyle O'X'}$ ardatzetan zehar higitzen den argi-izpi bat. Argi-izpiaren abiadura ${\displaystyle c}$ izango denez (edo ${\displaystyle v=-c}$ aurkako noranzkoan badoa), eta igorpena ${\displaystyle (t_{0},x_{0})\approx (t_{0}',x_{0}')}$ gertaera bada, bi sistemen unibertso-lerroak hauek dira:

${\displaystyle c(t-t_{0})=\pm (x-x_{0})}$

${\displaystyle c(t'-t_{0}')=\pm (x'-x_{0}')}$

Honen bitartez, argi ikusten da fotoiaren unibertso lerroa ${\displaystyle \pm 1}$ maldako unibertso-lerroa dela sistema-inertzial guztietan.

Lorentzen transformazioen ondorioak

Erlatibitate bereziaren ondorioak Lorentzen transformazioen bidez azter daitezke^[5]. Erlatibitate berezian lorturiko emaitzak ez datoz bat mekanika newtondarrarekin lortzen diren emaitzekin (zeinak Galileoren transformazioetan oinarritzen diren). Gorputzen abiadurak argiarena baino askoz txikiagoak direnean, Galileoren transformazioak hurbilketa egokiak dira. Argiaren abiadura oso handia denez, erlatibitate bereziaren ondorioak ez dira hautematen eguneroko egoeretan. Hori dela eta, ez dira intuitiboak izaten.

Denboraren zabalkuntza

Bi gertaeren arteko denbora-tartea ez da absolutua, erreferentzia-sistemaren mendekoa baizik. Demagun S' sisteman geldi dagoen erloju bat. Bi momenturen gertaerak modu honetan karakteriza daitezke: ${\displaystyle G'_{1}(x'_{1},t'_{1})}$ eta ${\displaystyle {\displaystyle G'_{2}(x'_{2},t'_{2})}}$. Nabaria denez, igarotako denbora ondorengoa izango da: ${\displaystyle \Delta t'=\Delta t'_{2}-\Delta t'_{1}}$. Bestalde, erlojua geldi dagoenez: ${\displaystyle \Delta x'=x'_{2}-x'_{1}=0}$. ${\displaystyle S}$ erreferentzia-sisteman, berriz, gertaerak ${\displaystyle G_{1}(x_{1},t_{1})}$ eta ${\displaystyle G_{2}(x_{2},t_{2})}$ gisa karakterizatzen dira, eta denbora eta espazio tarteak ${\displaystyle \Delta t=\Delta t_{2}-\Delta t_{1}}$ eta ${\displaystyle \Delta x=x_{2}-x_{1}}$ izango dira. Lorentzen transformazioak erabiliz, ${\displaystyle \Delta t}$ kalkula daiteke:

${\displaystyle \Delta t=\gamma (\Delta t'-{\frac {v}{c^{2}}}\Delta x')=\gamma \Delta t'}$

${\displaystyle \gamma >1}$ denez beti, ${\displaystyle \Delta t>\Delta t'}$ izango da. Beste modu batean esanda, ${\displaystyle S}$ sistemako behatzaileak neurtzen duen denbora tartea bi gertaeren artean handiagoa izango da ${\displaystyle S'}$ sistemako behatzaileak neurtzen duena baino. Fenomeno honi denboraren zabalkuntza deritzo.

Fitz-gerald eta Lorentzen uzkurdura

Denbora ez ezik, distantziak ere behatzailearen araberakoak dira. Jo dezagun, ${\displaystyle S}$ erreferentzia-sisteman, ${\displaystyle L}$ luzerako hagaxka bat higitzen dela ${\displaystyle v}$ abiadura konstantean. Luzera hori neurtzeko mutur bakoitzaren posizioa neurtu behar da aldiune berean. Hurrengo eran adieraz daitezke neurketak: ${\displaystyle G_{1}(x_{1},t_{1})}$ eta ${\displaystyle G_{2}(x_{2},t_{2})}$.

Nabaria denez, ${\displaystyle \Delta x=x_{2}-x_{1}=L}$ eta ${\displaystyle \Delta t=t_{2}-t_{1}=0}$

Orain, kontsidera ditzagun hagaxkarekin batera higitzen den ${\displaystyle S'}$ erreferentzia sistemako ${\displaystyle G'_{1}(x'_{1},t'_{1})}$ eta ${\displaystyle G'_{2}(x'_{2},t'_{2})}$ gertaerak. Sistema horretako behatzaile batek neurtuko duen barraren distantzia Lorentzen transformazioen bidez ${\displaystyle \Delta x'=x'_{2}-x'_{1}}$ kalkula daiteke:

${\displaystyle \Delta x'=\gamma (\Delta x-v\Delta t)=\gamma \Delta x=\gamma L}$

Beraz, hagaxkarekin batera mugitzen den behatzaileak luzera handiagoa neurtuko du barra mugitzen ikusten duen behatzaileak baino. Beste era batean esanda, behatzailearekiko abiadura erlatiboa duten objektuak uzkurtu egiten dira. Fenomeno honi Fitz-gerald eta Lorentzen uzkurdura deritzo.

Aldiberekotasunaren erlatibitatea

Lorentzen transformazioen beste ondorio zuzen bat da aldiberekotasuna erlatiboa izatea; hots, ezin esan dezakegu absolutuki bi gertaera leku banatan aldiberean gertatu direnik. Kontzeptu hori hobeto ulertzeko, Einsten-en ohiturari jarraituz, buru-esperimentu bat egingo dugu.

Demagun tren bateko bagoi baten muturretan detektagailu bana jarri dugula, ${\displaystyle D_{1}}$ eta ${\displaystyle D_{2}}$. Are gehiago, demagun bagoiaren erdian mutur bietara argia igortzen duen iturri bat jarri dugula. Bestalde, jo dezagun bagoian behatzaile bat dagoela: ${\displaystyle O'}$. Behatzaile horrentzat argi-izpiak aldi berean helduko dira ${\displaystyle D_{1}}$ eta ${\displaystyle D_{2}}$ detektagailuetara, ${\displaystyle \Delta t'={\frac {l}{2c}}}$ denbora igarota ( l${\displaystyle l}$ bagoiaren luzera da).

Orain, demagun kanpoan beste behatzaile bat dagoela, ${\displaystyle O}$. Behatzaile horrek argia c abiaduran higitzen dela ikusiko du. Gainera, trena v abiaduran higitzen bada, berebat ikusiko du ${\displaystyle D_{2}}$ detektorea argi-izpirantz ${\displaystyle v}$ abiaduran hurbiltzen dela; ${\displaystyle D_{1}}$ detektorea igorritako argitik ${\displaystyle v}$ abiaduran urruntzen den bezala. Hori horrela, argi-izpiek, detektagailuetara heltzeko, denbora hau beharko dute:

${\displaystyle \Delta t_{D_{1}}={\frac {{\frac {l}{2}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}{c-v}}}$

${\displaystyle \Delta t_{D_{2}}={\frac {{\frac {l}{2}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}{c+v}}}$

Ikus daiteke ${\displaystyle O}$ behatzailearentzat izpiak ez direla aldi berean heltzen bi detektagailuetara. Argi-izpia ${\displaystyle D_{2}}$ detektagailura heldu eta denbora-tarte bat igarota heltzen da ${\displaystyle D_{1}}$detektagailura:

${\displaystyle \Delta t_{D1}-\Delta t_{D2}={\frac {\frac {lv}{c^{2}}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}$

Buru-esperimentu honen bidez, argi ikusten da behatzaile batentzat bi gertaera aldiberekoak direla, baina beste erreferentzia-sistema bateko behatzaile batentzat ez dela horrela gertatzen.  Beraz, erlatibitate bereziaren ondorio garrantzitsu bat  aztertu dugu: erreferentzia-sistema inertzial ezberdinetan gertaera berdinak denbora-tarte ezberdinetan jazo daitezke. Beste era batera esanda, baliteke ${\displaystyle S}$ sisteman ${\displaystyle G_{1}}$ eta ${\displaystyle G_{2}}$ gertaerak aldi berean neurtu eta ${\displaystyle S'}$sisteman ${\displaystyle G_{1}}$ ${\displaystyle G_{2}}$ baino arinago neurtu izana; are gehiago, beste erreferentzia-sistema batean ( ${\displaystyle S''}$ ) ${\displaystyle G_{2}}$ ${\displaystyle G_{1}}$ baino arinago neurtu izana.

Bikien paradoxa

Bikien paradoxa Lorentzen transformazioen ondorio den esperimentu mentala da. Esperimentu hori Einsteinek proposatu zuen denbora absolutua ez dela frogatzeko asmotan. Paradoxa honek aldaera asko ditu; ezagunena Paul Langevin-ek proposatu zuen 1911. urtean. Aldaera honako eran azalduko dugu.

Esperimentu horretako protagonistak biki bi dira (Ane eta Beñat, adibidez). Ane izar urrun batera doa bidaian, ia argiaren abiaduran doan espazio-ontzi batean; Beñat, berriz, Lurrean geratu da. Bueltatzen denean, Ane bikia baino gazteagoa dela konturatzen da.

Orain arte, inplizituki, Lurrean dagoen bikiaren ikuspuntutik ebatzi dugu proposatutako problema. Baina, zer gertatzen da espazio-ontzian doan bikiaren ikuspuntutik ebazten badugu? Hona hemen paradoxa. Espazio-ontzian doan bikiaren ikuspuntutik, Lurrean dagoen bikia da aldenduz doana eta, ondorioz, azkarrago zahartuko den bikia espazio-ontzikoa izango da.

Einsteinek, paradoxa honi, erlatibitate berezia eraiki zuenean eman zion erantzuna. Hala ere, atal honetan, paradoxa erlatibitate bereziaren limiteetan ebatziko dugu. Paradoxa argitzeko, kalkuluak bi bikien ikuspuntua kontuan hartuz egingo ditugu, hala Lurreko bikiaren ikuspuntutik, nola espazio-ontziko bikiaren ikuspuntutik.

Lurrean geratzen den bikiaren ikuspuntutik, probleman bost gertaeratan bana daiteke:

1. ${\displaystyle t=0}$ unean, espazio-ontziko bikia ${\displaystyle \omega ={\frac {F}{m}}}$ “sasiazelerazio”  konstantearekin irtengo da Lurretik izarrerantz. Lurrean neurtutako ${\displaystyle t=0}$ eta ${\displaystyle t=T_{1}}$ denbora-tartean, azeleratu egingo da V abiadura lortu arte.
2. ${\displaystyle V}$ abiadura lortzen duen unean, bikiak motorrak itzaliko ditu, eta abiadura konstantean higituko da Lurreko bikiarekiko. Hau guztia lurrean neurtutako ${\displaystyle t=T_{1}}$ eta ${\displaystyle t=T_{1}+T_{2}}$ denbora-tartean gertatuko da.
3. Abiadura uniformean bidaiatu ondoren, bikiak martxan jarriko ditu berriro espazio-ontziaren motorrak; baina, oraingoan, aurkako noranzkoan eta hasieran izandako “sasiazelerazio” berberarekin desazeleratuko da. Horrela, ${\displaystyle t=T_{1}}$ denbora pasatuta (betiere Lurretik neurtua) abiadura nulua izango da, eta beste ${\displaystyle t=T_{1}}$ denbora-tarte bat igarota, abiadura ${\displaystyle -v}$ izango da.
4. ${\displaystyle -v}$ abiadura lortuta, bikia abiadura uniformean hurbilduko da Lurrerantz, ${\displaystyle t=T_{2}}$ denbora tarte batez.
5. Azkenik, Lurreko bikiarengana itzuli ahal izateko espazio-ontziko bikiak beste desazelerazio bat jasango du, ${\displaystyle t=T_{1}}$ denbora tartez

Gertaera horiek guztiak kontuan hartuz, Lurreko behatzailearen ikuspuntutik, honako hau da espazio-ontziko bikiak bidaiatzen emandako denbora:

${\displaystyle T_{bidaia}=T_{1}+(T_{1}+T_{2}-T_{1})+(T_{1}+T_{1})+T_{2}+T_{1}=4T_{1}+2T_{2}}$

Orain, kalkulatuko dugu zenbat uste duen espazio-ontziko bikiak bidaiak iraun duela Lurreko bikiak egindako neurketaren arabera. Kalkulu horiek egiteko, problema pauso desberdinetan banatuko dugu berriro ere:

1. Hasiera batean sasiazelerazioaren eta higidura azeleratu erlatibistaren arteko erlazioa erabilita kalkula dezakegu Lurrean dagoen bikiak estimatuko duen denbora:

${\displaystyle {\overline {T_{1}}}=\int _{0}^{T_{1}}{\frac {1}{\sqrt {1+{\frac {\omega ^{2}t^{2}}{c^{2}}}}}}dt={\frac {c}{\omega }}\ln \left({\frac {\omega T_{1}}{c}}+{\sqrt {1+{\frac {\omega ^{2}T_{1}^{2}}{c^{2}}}}}\right)}$

2. ${\displaystyle t=T_{1}}$ eta ${\displaystyle t=T_{1}+T_{2}}$ espazio-ontzia ${\displaystyle v}$ abiadura uniformean higitzen da; beraz:

${\displaystyle {\overline {T_{2}}}=\int _{T_{1}}^{T_{1}+T_{2}}{\sqrt {1-{\frac {V^{2}}{c^{2}}}}}dt={\frac {T_{2}}{\sqrt {1+{\frac {\omega ^{2}T_{1}^{2}}{c^{2}}}}}}}$

3. Espazio-ontzikoak bere bikiak  honako denbora hau neurtu duela uste du:

${\displaystyle {\overline {T_{bidaia}}}=4{\overline {T_{1}}}+2{\overline {T_{2}}}={\frac {4c}{\omega }}\ln \left({\frac {\omega T_{1}}{c}}+{\sqrt {1+{\frac {\omega ^{2}T_{1}^{2}}{c^{2}}}}}\right)+{\frac {2T_{2}}{\sqrt {1+{\frac {\omega ^{2}T_{1}^{2}}{c^{2}}}}}}}$

Ikus daiteke edozein ${\displaystyle \omega }$, ${\displaystyle T_{1}}$ eta ${\displaystyle T_{2}}$ izanda ${\displaystyle T_{bidaia}-{\overline {T_{bidaia}}}>0}$ dela.  Hau da, problema Lurreko bikiaren ikuspuntutik ebazten badugu,haren iritziz, bera bere bikia baino azkarrago zahartuko da.

Kalkuluak espazio-ontziko bikiaren ikuspuntutik egitea zailagoa da, eta ez ditugu egingo; izan ere, haren erreferentzia-sistema ez da inertziala. Hala ere, ikus daiteke Lurrean dagoen bikiaren ikuspuntutik lortutako emaitza bera lortzen dela.

Problema ebatziz, bi ondorio nagusi atera daitezke:

1. Erreferentzia-sistema inertzialean egindako kalkuluen emaitza eta erreferentzia-sistema ez-inertzialean egindakoenak berdinak dira; bi bikiek Lurreko bikia arinago zahartuko dela ondorioztatu dute.
2. Paradoxa erlatibitate bereziaren limiteetan aska daiteke, erlatibitate orokorrera jo gabe; baina kontu handia izan behar da erreferentzia-sistema inertzialekin eta metrika ez haustearekin.

Momentu lineal erlatibista

Sistema bakartuen momentu lineal osoaren kontserbazioa fisikaren funtsezko kontzeptu bat da. Hori beteko bada, momentuaren definizioa berregokitu behar da, lehenengo postulatuarekin baliagarri izan dadin. Mekanika newtondarrean honela definitzen da momentu lineala:

${\displaystyle {\vec {p}}=m{\dot {\vec {r}}}}$

Bi partikulaz osaturiko sistema baten hasierako eta amaierako momentuak berdinak izango dira:

${\displaystyle m_{1}{\dot {\vec {r_{1}}}}+m_{2}{\dot {\vec {r_{2}}}}=m_{3}{\dot {\vec {r_{3}}}}+m_{4}{\dot {\vec {r_{4}}}}}$

Lehenengo postulatuaren arabera, fisikaren oinarrizko legeek forma bera izan behar dute erreferentzia sistema guztietan; hortaz, Lorentzen transformazio bat aplikatzean, kontserbazio-printzipioak itxura bera mantendu beharko luke. Hasierako ${\displaystyle S}$ sistemarekiko ${\displaystyle v}$ abiaduran higitzen den ${\displaystyle S'}$sistematik behatuz gero, honako balio hauek neurtzen dira:

${\displaystyle m_{1}{\frac {\sqrt {{}1-{\frac {|{\vec {r_{1}}}|^{2}}{c^{2}}}}}{\sqrt {{}1-{\frac {|{\vec {r'_{1}}}|^{2}}{c^{2}}}}}}{\dot {\vec {r'_{1}}}}+m_{2}{\frac {\sqrt {{}1-{\frac {|{\vec {r_{2}}}|^{2}}{c^{2}}}}}{\sqrt {{}1-{\frac {|{\vec {r'_{2}}}|^{2}}{c^{2}}}}}}{\dot {\vec {r'_{2}}}}=m_{3}{\frac {\sqrt {{}1-{\frac {|{\vec {r_{3}}}|^{2}}{c^{2}}}}}{\sqrt {{}1-{\frac {|{\vec {r'_{3}}}|^{2}}{c^{2}}}}}}{\dot {\vec {r'_{3}}}}+m_{4}{\frac {\sqrt {{}1-{\frac {|{\vec {r_{4}}}|^{2}}{c^{2}}}}}{\sqrt {{}1-{\frac {|{\vec {r'_{4}}}|^{2}}{c^{2}}}}}}{\dot {\vec {r'_{4}}}}}$

Horrek ez du hasierako kontserbazio-printzipioaren antzik. Hori konpontzeko momentu linealaren definizioa aldatu behar da:

${\displaystyle {\vec {p}}=m\gamma {\dot {\vec {r}}}={\vec {p}}=m{\frac {1}{\sqrt {1-{\frac {|{\vec {r}}|^{2}}{c^{2}}}}}}{\dot {\vec {r}}}}$

Modu honetan, kontserbazio-printzipioa horrela idatzi daiteke ${\displaystyle S}$ erreferentzia-sisteman:

${\displaystyle m_{1}\gamma _{1}{\dot {\vec {r_{1}}}}+m_{2}\gamma _{2}{\dot {\vec {r_{2}}}}=m_{3}\gamma _{3}{\dot {\vec {r_{3}}}}+m_{4}\gamma _{4}{\dot {\vec {r_{4}}}}}$

${\displaystyle \gamma _{i}={\frac {1}{\sqrt {1-{\frac {|{\vec {r_{i}}}|^{2}}{c^{2}}}}}}}$

Eta ${\displaystyle S'}$erreferentzia-sisteman:

${\displaystyle m_{1}\gamma _{1}{\dot {\vec {r'_{1}}}}+m_{2}\gamma _{2}{\dot {\vec {r'_{2}}}}=m_{3}\gamma _{3}{\dot {\vec {r'_{3}}}}+m_{4}\gamma _{4}{\dot {\vec {r'_{4}}}}}$

${\displaystyle \gamma _{i}={\frac {1}{\sqrt {1-{\frac {|{\vec {r'_{i}}}|^{2}}{c^{2}}}}}}}$

Momentuaren definizio berri honekin kontserbazio legea bateragarria bihurtzen da lehenengo postulatuarekin. Limite galilearrean, momentuaren definizio klasikoa berreskuratzen dugu, espero bezala:

${\displaystyle {\frac {v}{c}}\approx 0\Rightarrow \gamma \approx 1\Rightarrow {\vec {p}}\approx m{\vec {v}}}$

Masa eta energia

Energiaren kontserbazio-printzipoak dioen bezala, sistema bakartuen energia osoa kontserbatu egiten da. Erlatibitate berezian, energiak forma ezberdinak hartzen ditu. Horren adibide honakoa dugu:

${\displaystyle E=m\gamma c^{2}}$

Energiaren adierazpen hori partikula bakartu baten energia osoa da (kanpo-eremu baten mende badago, dagokion energia potentziala batu behar zaio energiari).

Adierazpenaren Taylorren garapena egiten badugu:

${\displaystyle E=m\gamma c^{2}=mc^{2}+{\frac {1}{2}}m{\dot {\vec {r}}}^{2}+{\frac {3}{8}}m{\frac {{\dot {\vec {r}}}^{4}}{c^{2}}}+...}$

Limite galilearrean, adierazpenaren lehenengo bi terminoak geratuko zaizkigu soilik:

${\displaystyle E=m\gamma c^{2}\approx mc^{2}+{\frac {1}{2}}m{\dot {\vec {r}}}^{2}}$

Hori da, hain zuzen ere, energia zinetikoaren eta gai konstante baten arteko batura (gogoratu, mekanika newtondarrean ere, energiaren balio zehatzek ez dutela esangura fisikorik; energia aldaketek dute soilik garrantzia). Gai konstante horri partikularen pausaguneko energia (${\displaystyle E_{0}}$) deritzo, eta ${\displaystyle m}$ kantitateari ordea, pausaguneko masa.

${\displaystyle E_{0}=mc^{2}}$

Azkenik, energia osoaren adierazpena eta momentuaren definizioa konbinatzen baditugu, ${\displaystyle \gamma }$ faktore gabeko energia osoaren adierazpena lortuko dugu:

${\displaystyle E^{2}=(mc^{2})^{2}+(pc)^{2}}$

Masaren terminoa askatuta, honela geratzen da adierazpena:

${\displaystyle E^{2}-p^{2}c^{2}=m^{2}c^{4}}$

Eskuineko aldea konstantea denez, ezkerreko aldeak ere konstantea izan behar du, eta beraz, erreferentzia-sistema guztietan balio berbera izan behar du. Hau da, azken adierazpen hori aldaezin erlatibista da.

Bibliografia

• Aguirregabiria, Juan María.. (2004). Mekanika klasikoa. Universidad del País Vasco ISBN 84-8373-631-4. PMC 932541663. (Noiz kontsultatua: 2019-12-04).

Erreferentziak

Kanpo estekak

• Datuak: Q11455
• Multimedia: Special relativity / Q11455