Puissance parfaite

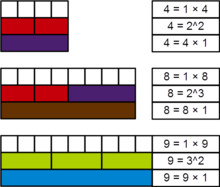
En mathématiques, une puissance parfaite est un entier naturel qui peut être exprimé sous la forme d'un carré ou d'une puissance entière supérieure ou égale à 2 d'un entier lui aussi supérieur ou égal à 2. Plus formellement, n est une puissance parfaite s'il existe des entiers naturels ${\displaystyle a\geqslant 2}$, et ${\displaystyle k\geqslant 2}$ tels que ${\displaystyle n=a^{k}}$ . Dans ce cas, n est appelé une puissance k-ième parfaite . Si k = 2 ou k = 3, n est appelé un carré parfait ou un cube parfait. Parfois, 0 et 1 sont également considérés comme des puissances parfaites (puisque 0^k = 0 pour tout k > 0, 1^k = 1 pour tout k ).

Exemples et sommes

La liste croissante des puissances parfaites (en conservant les répétitions) est donnée par la suite A072103 de l'OEIS :

${\displaystyle 2^{2}=4,\ 2^{3}=8,\ 3^{2}=9,\ 2^{4}=16,\ 4^{2}=16,\ 5^{2}=25,\ 3^{3}=27,}$ ${\displaystyle 2^{5}=32,\ 6^{2}=36,\ 7^{2}=49,\ 2^{6}=64,\ 4^{3}=64,\ 8^{2}=64,\dots }$

La somme des inverses des puissances parfaites (y compris les doublons tels que 3 ⁴ et 9 ², tous deux égaux à 81) est égale à 1 :

${\displaystyle \sum _{a=2}^{\infty }\sum _{k=2}^{\infty }{\frac {1}{a^{k}}}=1.}$

ce qui peut se montrer comme suit :

${\displaystyle \sum _{a=2}^{\infty }\sum _{k=2}^{\infty }{\frac {1}{a^{k}}}=\sum _{a=2}^{\infty }{\frac {1}{a^{2}}}\sum _{k=0}^{\infty }{\frac {1}{a^{k}}}=\sum _{a=2}^{\infty }{\frac {1}{a^{2}}}\left({\frac {a}{a-1}}\right)=\sum _{a=2}^{\infty }{\frac {1}{a(a-1)}}=\sum _{a=2}^{\infty }\left({\frac {1}{a-1}}-{\frac {1}{a}}\right)=1\,.}$

La liste où l'on a supprimé les répétitions :

(parfois 0 et 1), 4, 8, 9, 16, 25, 27, 32, 36, 49, 64, 81, 100, 121, 125, 128, 144, 169, 196, 216, 225, 243, 256, 289, 324, 343, 361, 400, 441, 484, 512, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1000, 1024, ... suite A001597 de l'OEIS

La somme des inverses des puissances parfaites sans répétitions est  :

${\displaystyle \sum _{n\in P}{\frac {1}{n}}=\sum _{k=2}^{\infty }\mu (k)(1-\zeta (k))\approx 0,874464368\dots }$

où ${\displaystyle P}$ est l'ensemble des puissances parfaites, μ est la fonction de Möbius et ζ la fonction zêta de Riemann ; voir la suite A072102 de l'OEIS.

Selon Euler, Goldbach a montré (dans une lettre aujourd'hui perdue) que la somme des 1/n − 1 où n décrit l'ensemble des puissances parfaites, excluant 1 et excluant les répétitions, est égale à 1 :

${\displaystyle \sum _{n\in P}{\frac {1}{n-1}}={{\frac {1}{3}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{15}}+{\frac {1}{24}}+{\frac {1}{26}}+{\frac {1}{31}}}+\cdots =1.}$

On trouvera sur la page : théorème de Goldbach-Euler la "démonstration" originelle de Goldbach, non conforme aux standards actuels de rigueur, ainsi qu'une démonstration se ramenant à la somme des inverses des puissances parfaites avec les répétions données ci-dessus.

Détecter les puissances parfaites

Déterminer si oui ou non un entier naturel donné n est une puissance parfaite peut être accompli de différentes manières, avec différents niveaux de complexité. L'une des méthodes les plus simples consiste à considérer toutes les valeurs possibles de k sur chacun des diviseurs de n, jusqu'à ${\displaystyle k\leqslant \log _{2}n}$ . Donc si les diviseurs de ${\displaystyle n}$ sont ${\displaystyle n_{1},n_{2},\dots ,n_{j}}$ alors une des valeurs ${\displaystyle n_{1}^{2},n_{2}^{2},\dots ,n_{j}^{2},n_{1}^{3},n_{2}^{3},\dots }$ doit être égal à n si n est une puissance parfaite.

Cette méthode peut être immédiatement simplifiée en ne considérant que les valeurs premières de l'entier k . En effet, si ${\displaystyle n=a^{k}}$ pour un nombre composé ${\displaystyle k=dp}$ où p est premier, alors cela peut simplement être réécrit sous la forme ${\displaystyle n=a^{k}=a^{dp}=(a^{d})^{p}}$ . Grace à ce résultat, la valeur minimale de k est nécessairement première.

Si la factorisation complète de n est connue, disons ${\displaystyle n=p_{1}^{\alpha _{1}}p_{2}^{\alpha _{2}}\cdots p_{r}^{\alpha _{r}}}$ où les ${\displaystyle p_{i}}$ sont des nombres premiers distincts, alors n est une puissance parfaite si et seulement si ${\displaystyle \operatorname {pgcd} (\alpha _{1},\alpha _{2},\ldots ,\alpha _{r})>1}$ où pgcd désigne le plus grand diviseur commun. Par exemple, considérons n = 2 ⁹⁶ ·3 ⁶⁰ ·7 ²⁴ . Puisque pgcd(96, 60, 24) = 12, n est une puissance douzième parfaite (et une puissance sixième, quatrième, un cube et un carré parfaits, puisque 6, 4, 3 et 2 divisent 12).

Écarts entre puissances parfaites

En 2002, le mathématicien roumain Preda Mihăilescu a montré que la seule paire de puissances parfaites consécutives est 2 ³ = 8 et 3 ² = 9, prouvant ainsi la conjecture de Catalan.

La conjecture de Pillai stipule que pour tout entier positif k donné, il n'y a qu'un nombre fini de paires de puissances parfaites dont la différence est k . C'est un problème non résolu.

Voir aussi

• Les nombres primaires (puissances d'un nombre premier)
• Les nombres puissants (où les ${\displaystyle \alpha _{i}}$ sont ${\displaystyle >1}$), qui généralisent les puissances parfaites.
• Carré parfait
• Cube parfait
• Puissance quatrième parfaite

Références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Perfect power » (voir la liste des auteurs).

• Daniel J. Bernstein, « Detecting perfect powers in essentially linear time », Mathematics of Computation, vol. 67, n^o 223,‎ 1998, p. 1253–1283 (DOI 10.1090/S0025-5718-98-00952-1, lire en ligne)

Liens externes

• Lluís Bibiloni, Pelegrí Viader et Jaume Paradís, Sur une série de Goldbach et Euler, 2004 (Pdf)

• Portail des mathématiques