Perdület

A perdület, más néven impulzusnyomaték, vagy impulzusmomentum a klasszikus fizikában egy test forgási mozgásállapotát jellemző vektormennyiség.

Jele: N, mértékegysége a kg•m²/s, vagy az ezzel ekvivalens N•m•s. Jele a IUPAC dokumentumaiban L.

A kvantummechanikában az impulzusmomentum a hullámfüggvény forgatásokkal szembeni viselkedését leíró mennyiség. A nulla impulzusmomentum például azt jelenti, hogy a hullámfüggvény a forgatás során változatlan marad, azaz forgásszimmetrikus.

A klasszikus mechanikában

Definíció

Egy mozgó tömegpont adott pontra vonatkoztatott perdületét az alábbi kifejezés adja meg: ${\displaystyle \mathbf {N} =\mathbf {r} \times \mathbf {p} }$, ahol ${\displaystyle \mathbf {r} }$ a tömegpont adott vonatkoztatási pontból mért helyvektora, és ${\displaystyle \mathbf {p} }$ a lendülete, azaz a tömeg és a sebesség szorzata.^[1]

A vektorszorzat definíciója alapján az ${\displaystyle \mathbf {r} }$, a ${\displaystyle \mathbf {p} }$ és az ${\displaystyle \mathbf {N} }$ vektorok jobbsodrású vektorrendszert alkotnak, és az impulzusnyomaték nagysága a következő szerint számolható:

${\displaystyle N={r}\cdot {p}\cdot \sin \theta _{r,p}}$, ahol ${\displaystyle \theta _{r,p}}$ a helyvektor és az impulzus által bezárt szög.

Több tömegpontból álló rendszer adott pontra vonatkoztatott teljes perdülete az egyes pontok perdületeinek vektori eredője:

${\displaystyle \mathbf {N} =\sum _{i}\mathbf {N} _{i}=\sum _{i}(\mathbf {r} _{i}\times \mathbf {p} _{i})}$

Merev testek rögzített tengely körüli forgása esetén az impulzusnyomatékot a fenti vektorszorzat helyett egyszerűbb alakban is felírhatjuk:

${\displaystyle {N}=\Theta \cdot \omega }$, ahol ${\displaystyle \omega }$ a forgás szögsebessége és ${\displaystyle \theta }$ a test adott tengelyre vonatkozó tehetetlenségi nyomatéka.

A perdülettétel, azaz a perdület megváltozása és a forgatónyomaték

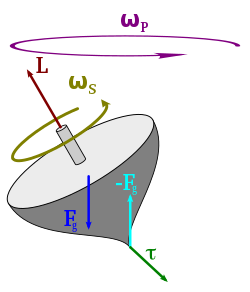
Legyen egy tömegpont esetén a rá ható ${\displaystyle \mathbf {F} }$ erő adott pontra vonatkozó forgatónyomatéka: ${\displaystyle \mathbf {M} =\mathbf {r} \times \mathbf {F} }$, ahol a forgatónyomatékot az animáción ${\displaystyle \mathbf {\tau } }$-val jelölt helyett a szokásosabb ${\displaystyle \mathbf {M} }$ jelöli. A perdülettétel szerint a perdület megváltozását a forgatónyomaték okozza, és a perdület idő szerint deriváltja megegyezik a forgatónyomatékkal. Tehát: ${\displaystyle \mathbf {\frac {dN}{dt}} =\mathbf {M} }$.

A perdület megmaradásának törvénye

A fentiek alapján, ha a forgatónyomatékok eredője nulla, akkor a perdület állandó: ${\displaystyle \sum \mathbf {M} =0\rightarrow \mathbf {\frac {dN}{dt}} =0\rightarrow \mathbf {N} =\mathrm {const.} }$ Ez a perdületmegmaradás törvénye.

Merev test forgásegyenlete

Merev test tengely körüli forgásánál az impulzusnyomaték a tehetetlenségi nyomaték és a szögsebesség szorzata, ezért a perdület időbeli deriváltja a következő alakban is felírható:

${\displaystyle {\frac {dN}{dt}}={\frac {d(\theta \cdot \omega )}{dt}}=\theta {\frac {d\omega }{dt}}=\theta \cdot \beta }$, ahol ${\displaystyle \beta }$ a test forgásához tartozó szöggyorsulás.

A perdülettétel ebben az esetben a test forgását leíró egyenlet, az úgynevezett forgásegyenlet is egyben:

${\displaystyle \theta \cdot \beta =M}$

Ha a forgatónyomatékok eredője zérus, akkor a szöggyorsulás is zérus, azaz a merev test állandó szögsebességgel forog: ${\displaystyle M=0\rightarrow \beta ={\frac {d\omega }{dt}}=0\rightarrow \omega =\mathrm {const.} }$

A perdületmegmaradás alkalmazásai

Amikor egy forgásban levő korcsolyázó a lábait és a karjait behúzza a törzséhez, a mozdulat során csökken a tehetetlenségi nyomatéka. Mivel külső forgatónyomaték nem hat rá, a perdületmegmaradás miatt a szögsebessége nőni fog, azaz forgása felgyorsul.

Ugyanez a helyzet az igen nagy sebességgel forgó kompakt csillagok, például a fehér törpék, neutroncsillagok és fekete lyukak esetén is, amikor azok sokkal nagyobb, lassabban forgó csillagokból keletkeznek. Így egy csillag nagyságának 10⁴-ed részére való lecsökkenése forgási sebességének 10⁸-szorosával való növekedését eredményezi.

A perdület megmaradása miatt a Föld–Hold rendszer esetében a Hold által okozott dagály a Hold keringési sebességének növekedésével jár, mivel a Föld a Holdnak átadja perdületének egy részét. Ahogy a Hold felgyorsul, a Föld lelassul, mégpedig egy nap alatt 42 nanomásodperccel, ugyanakkor a Hold keringési távolsága is megnő, mégpedig évente kb. négy és fél centiméterrel.

Centrális erőtér és a perdületmegmaradás

Amennyiben a testre ható erők eredője centrális, azaz a test mozgása közben mindig egy adott pont felé mutat, akkor az erre a pontra vonatkoztatott forgatónyomaték zérus. Így az erre a pontra vonatkozó impulzusmomentum megmarad.

Impulzusnyomaték a tömegközépponti rendszerben

Több pontból álló rendszer esetén az impulzusnyomaték a tömegközéppont mozgásának ismeretében két részre bontható.^[2] Magának a tömegközéppontnak a mozgásához tartozó pálya-impulzusmomentumra, és a rendszer tagjainak ehhez viszonyított mozgásához tartozó saját-impulzusmomentumra. Ez utóbbit nevezzük spinnek.

${\displaystyle \mathbf {N} _{\mathrm {teljes} }=\mathbf {N} _{\mathrm {spin} }+\mathbf {N} _{\mathrm {palya} }}$

A relativisztikus mechanikában

Ez a szakasz egyelőre üres vagy erősen hiányos. Segíts te is a kibővítésében!

A kvantummechanikában

A kvantummechanikában a perdületet a lendülethez hasonlóan a hullámfüggvényen ható operátorként definiáljuk:

${\displaystyle {\hat {\mathbf {N} }}={\hat {\mathbf {r} }}\times {\hat {\mathbf {p} }}}$

Elektromos töltés és spin nélküli részecskére helyreprezentációban

${\displaystyle {\hat {\mathbf {N} }}=-i\hbar (\mathbf {r} \times \nabla )}$,

ahol r a részecske helye, ${\displaystyle \nabla }$ a gradiens operátor.

A perdület-operátorok algebrájának jellemző tulajdonságai az alábbi kommutátorok:

${\displaystyle [N_{i},N_{j}]=i\hbar \epsilon _{ijk}N_{k},\quad [N_{i},N^{2}]=0}$

L komponensei kommutálnak a spin és töltés nélküli részecske Hamilton-operátorával is, azaz megmaradó mennyiségek:

${\displaystyle \left[N_{i},H\right]=0}$

A perdület-operátor gyakran előfordul gömbszimmetrikus problémák megoldásakor. Gömbi koordináta-rendszerben, a helyreprezentációt használva az operátor alakja:

${\displaystyle N^{2}={\frac {1}{\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial }{\partial \theta }}\right)+{\frac {1}{\sin ^{2}\theta }}{\frac {\partial ^{2}}{\partial \phi ^{2}}}}$

L² és például L_z kommutál, ezért létezik közös sajátállapotrendszerük. Legyen egy ilyen állapotvektor |l,m>, ekkor a sajátértékegyenletek:

${\displaystyle N^{2}|n,m\rangle =\hbar ^{2}n(n+1)|n,m\rangle }$

${\displaystyle N_{z}|n,m\rangle =\hbar m|n,m\rangle }$

A sajátvektorok polárkoordináta-reprezentációban éppen a gömbfüggvények:

${\displaystyle \langle \theta ,\phi |n,m\rangle =Y_{l,m}(\theta ,\phi )}$

Mindez tulajdonképpen csak a perdület egy része, az ún. pályaperdület vagy pályamomentum. A relativisztikus kvantummechanikában megjelenik a spin, ami ilyen módon nem definiálható.

Jegyzetek

Források

• ↑ Landau I: L. D. Landau, E. M. Lifsic. Elméleti fizika - Mechanika. Tankönyvkiadó, Budapest (1974). ISBN 963 17 0436 X 
• ↑ Landau III: L. D. Landau, E. M. Lifsic. Elméleti fizika - Kvantummechanika. Tankönyvkiadó, Budapest (1978). ISBN 963 17 3259 2 

További információk

• Magyarított Flash prezentáció: a mindig talpra eső macska és a perdületmegmaradás. Szerző: David M. Harrison
• Magyarított Flash animáció egy precesszáló pörgettyűről. Szerző: David M. Harrison