Frattali per dimensione di Hausdorff

In matematica, un frattale è un oggetto geometrico in cui la dimensione di Hausdorff (δ) è strettamente superiore alla dimensione topologica. Qui di seguito è presentata una lista di frattali per dimensione di Hausdorff crescente, con lo scopo di visualizzare che cosa significhi per un frattale possedere una dimensione bassa o alta.

Frattali deterministici

δ (valore esatto)	δ (valore approssimato)	Nome	Commenti
${\frac {\ln(2)}{\ln(\delta _{F})}}$	$0,4498$	Biforcazioni dell'equazione logistica	Nel diagramma di biforcazione, all'avvicinarsi di ciascuna regione caotica, appare una successione di raddoppiamenti di periodo, in una progressione geometrica tendente a 1/δ. (δ_F=costante di Feigenbaum=4.6692).
${\frac {\ln(2)}{\ln(3)}}$	$0,6309$	Insieme di Cantor	Costruito eliminando la terza parte centrale ad ogni iterazione. Insieme mai denso, né numerabile.
${\frac {\ln(6)}{\ln(8)}}$	$0,8617$	Insieme di Smith-Volterra-Cantor	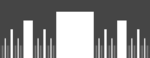Costruito eliminando la quarta parte centrale ad ogni iterazione. Insieme mai denso, ma avente misura di Lebesgue ½.
${\frac {\ln(8)}{\ln(7)}}$	$1,0686$	Isola di Gosper
	$1,26$	Attrattore di Hénon	L'attrattore di Hénon canonico (con parametri $a=1,4$ and $b=0,3$ ) possiede dimensione di Haussdorf δ = 1,261 ± 0,003. Parametri differenti conducono a differenti valori di δ.
${\frac {\ln(4)}{\ln(3)}}$	$1,2619$	Curva di Koch	3 di queste curve formano il fiocco o l'antifiocco di Koch.
${\frac {\ln(4)}{\ln(3)}}$	$1,2619$	Bordo della Curva Terdragon, Fudgeflake	L-System: simile alla curva del drago con un angolo di 30°. La Fudgeflake è costruita giustapponendo i 3 segmenti iniziali a formare un triangolo.
${\frac {\ln(4)}{\ln(3)}}$	$1,2619$	Polvere di Cantor in 2D	Insieme di Cantor in due dimensioni .
	$1,3057$	Setaccio di Apollonio
${\frac {\ln(5)}{\ln(3)}}$	$1,4649$	Scatola frattale	Costruito sostituendo iterativamente ciascun quadrato con una croce di 5 quadrati.
${\frac {\ln(5)}{\ln(3)}}$	$1,4649$	Curva di Koch quadratica (tipo 1)	In esso ritroviamo il motivo della scatola frattale (vedi sopra), costruito diversamente.
${\frac {\ln(8)}{\ln(4)}}$	$1,5$	Curva di Koch quadratica (tipo 2)	Chiamata anche "Salsiccia di Minkowski".
	$1,5236$	Bordo della Curva del Drago	Cf. Chang & Zhang^[1]
${\frac {\ln(3)}{\ln(2)}}$	$1,5850$	Albero a 3 rami	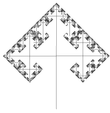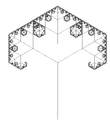Ogni ramo si divide in altri 3 rami. (qui i casi a 90° e 60°). La dimensione frattale dell'intero albero è quella dei rami terminali. NB: l'albero a 2 rami possiede dimensione frattale 1.
${\frac {\ln(3)}{\ln(2)}}$	$1,5850$	Triangolo di Sierpiński	Esso è anche il triangolo di Pascal modulo 2.
${\frac {\ln(3)}{\ln(2)}}$	$1,5850$	Curva di Sierpinski a punta di freccia	Stesso limite del triangolo di Sierpinski (vedi sopra), ma ottenuto per iterazione di costruito con una curva unidimensionale.
$1+\log _{3}(2)$	$1,6309$	Triangolo di Tartaglia modulo 3	In generale, per un triangolo modulo k, se k è primo, la dimensione frattale è $\scriptstyle {1+log_{k}({\frac {k+1}{2}})}$ (Cf.Stephen Wolfram^[2])
$1+\log _{5}(3)$	$1,6826$	Triangolo di Tartaglia modulo 5	Come sopra.
${\frac {\ln(7)}{\ln(3)}}$	$1,7712$	Fiocco esagonale	Costruito sostituendo iterativamente ogni esagono con un fiocco di 7 esagoni. Il suo bordo è il fiocco di Koch. Contiene infiniti fiocchi di Koch (bianchi e neri).
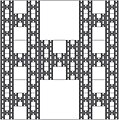
${\frac {\ln(7)}{\ln(3)}}$	$1,7712$	Frattale H-I di Rivera	Partendo da un quadrato unitario dividendo le sue dimensioni in tre parti uguali per formare nove quadrati autosimili con il primo quadrato, due quadrati centrali (quello che si trova sopra e quello sotto il quadrato centrale) vengono rimossi in ciascuno dei sette i quadrati non eliminati il processo viene ripetuto, quindi continua indefinitamente.
${\frac {\ln(4)}{\ln(2(1+\cos(85^{\circ }))}}$	$1,7848$	Curva di Koch a 85°, Frattale di Cesàro	Generalizzazione della curva di Koch con un angolo a scelta tra 0 e 90°. La dimensione frattale è allora $\scriptstyle {\frac {ln(4)}{ln(2(1+cos(a))}}$ . Il Frattale di Cesàro è basato su questo motivo.
${\frac {\ln(6)}{\ln(1+\phi )}}$	$1,8617$	Fiocco pentagonale	Costruito sostituendo iterativamente ogni pentagono con un fiocco di 6 pentagoni. Qui $\phi =\scriptstyle {\frac {1+{\sqrt {5}}}{2}}$ è il rapporto aureo.
${\frac {\ln(8)}{\ln(3)}}$	$1,8928$	Tappeto di Sierpinski
${\frac {\ln(8)}{\ln(3)}}$	$1,8928$	Polvere di Cantor in 3D	Insieme di Cantor in 3 dimensioni.
Stimato	$1,9340$	Bordo della Curva di Lévy	Stimato da Duvall and Keesling (1999). La curva di per sé possiede dimensione frattale 2.^{[non chiaro]}
	$1,974$	Tassellatura di Penrose	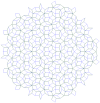Cf. Ramachandrarao, Sinha & Sanyal^[3]
$2$	$2$	Insieme di Mandelbrot	Qualsiasi oggetto piano contenente un disco possiede dimensione di Hausdorff δ = 2. Il bordo dell'insieme di Mandelbrot possiede ugualmente dimensione di Hausdorff δ = 2.
$2$	$2$	Curva di Sierpiński	Ogni curva che riempie il piano possiede dimensione di Hausdorff 2.
$2$	$2$	Curva di Hilbert	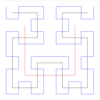Costruita in maniera simile: la curva di Moore
$2$	$2$	Curva di Peano	E una famiglia di curve costruite in maniera simile, come per esempio le curve di Wunderlich o le curve di Moore.
	$2$	Lebesgue curve or z-order curve	Contrariamente alle curve precedenti, questa è quasi ovunque differenziabile.
${\frac {\ln(2)}{\ln({\sqrt {2}})}}$	$2$	Curva del Drago	Il suo bordo possiede dimensione frattale 1,5236 (Cf.Chang & Zhang^[1]).
	$2$	Curva Terdragon	L-System : F-> F+F-F. angolo=120°.
${\frac {\ln(4)}{\ln(2)}}$	$2$	T-Square
${\frac {\ln(4)}{\ln(2)}}$	$2$	Curva di Peano-Gosper	Il suo bordo è l'Isola di Gosper.
${\frac {\ln(4)}{\ln(2)}}$	$2$	Tetraedro di Sierpinski
${\frac {\ln(4)}{\ln(2)}}$	$2$	H-fractal	Ugualmente, l'albero di Mandelbrot, che ha una struttura simile.
${\frac {\ln(4)}{\ln(2)}}$	$2$	2D greek cross fractal	Ogni segmento è sostituito da una croce formata da 4 segmenti.
	$2,06$	Attrattore di Lorenz	Per precisi valori dei parametri dell'attrattore.
${\frac {\ln(20)}{\ln(2+\phi )}}$	$2,3296$	Dodecaedro frattale	Ogni dodecaedro è sostituito da 20 dodecaedri. Qui $\phi =\scriptstyle {\frac {1+{\sqrt {5}}}{2}}$ è il rapporto aureo.
${\frac {\ln(13)}{\ln(3)}}$	$2,3347$	Superficie di Koch quadratica (tipo 1) in 3D	Estensione tridimensionale della curva di Koch quadratica (tipo 1). L'illustrazione mostra la seconda iterazione.
	$2,4739$	Interstizi delle sfere di Apollonio	Setaccio di Apollonio in 3 dimensioni. Imita la mollica di pane o la spugna. Dimensione calcolata da M. Borkovec, W. De Paris, and R. Peikert^[4].
${\frac {\ln(32)}{\ln(4)}}$	$2,5$	Superficie di Koch quadratica (tipo 2) in 3D	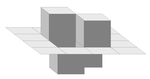Estensione tridimensionale della curva di Koch quadratica(tipo 2). L'illustrazione mostra la prima iterazione.
${\frac {\ln(16)}{\ln(3)}}$	$2,5237$	Ipercubo di Cantor	Insieme di Cantor in 4 dimensioni. In generale, in uno spazio di dimensione n, l'insieme di Cantor possiede dimensione di Hausdorff $\scriptstyle {n{\frac {ln(2)}{ln(3)}}}$
${\frac {\ln(12)}{\ln(1+\phi )}}$	$2,5819$	Icosaedro frattale	Ogni icosaedro è sostituito da 12 icosaedri. Qui $\phi =\scriptstyle {\frac {1+{\sqrt {5}}}{2}}$ è il rapporto aureo.
${\frac {\ln(6)}{\ln(2)}}$	$2,5849$	Frattale a croce greca in 3D	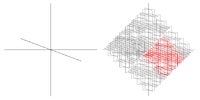Ogni segmento è sostituito con una croce formata da 6 segmenti. Estensione tridimensionale della croce in due dimensioni.
${\frac {\ln(6)}{\ln(2)}}$	$2,5849$	Ottaedro frattale	Ogni ottaedro è sostituito da 6 ottaedri.
${\frac {\ln(20)}{\ln(3)}}$	$2,7268$	Spugna di Menger	La sua superficie possiede dimensione frattale $\scriptstyle {{\frac {ln(20)}{ln(3)}}=2,7268}$ .
${\frac {\ln(8)}{\ln(2)}}$	$3$	Curva di Hilbert in 3D	Estensione tridimensionale della curva di Hilbert.

Frattali casuali e naturali

δ (valore esatto)	δ (valore approssimato)	Nome	Commenti
Misurato	$1,24$	Costa della Gran Bretagna
${\frac {4}{3}}$	$1,33$	Bordo del moto browniano	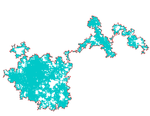(Cf Gregory Lawler, Oden Schramm et Wendelin Werner^[5]).
${\frac {4}{3}}$	$1,33$	Polimero 2D	Simile al moto browniano in 2D senza auto-intersezioni. (Cf Sapoval^[6]).
Misurato	$1,52$	Costa della Norvegia
Misurato	$1,55$	Camminata casuale senza intersezioni	Camminata casuale all'interno di un quadrato, con algoritmo di "ritorno" per evitare vicoli ciechi.
${\frac {5}{3}}$	$1,66$	Polimero 3D	Simile al moto browniano all'interno di un cubo, ma senza auto-intersezioni (Cf Sapoval^[6]).
$2$	$2$	Moto browniano	O camminata casuale. Le dimensioni di Hausdorff sono uguali a 2 in 2D, in 3D e in tutte le altre dimensioni (K.Falconer "The geometry of fractal sets").
${\frac {\ln(13)}{\ln(3)}}$	$2,33$	Cavolfiore	Ogni ramo porta 13 rami 3 volte più piccoli.
	$2,97$	Superficie polmonare	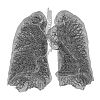Gli alveoli di un polmone formano una superficie frattale di dimensione vicina a 3 (Cf Sapoval^[6]).

Note

^ ^a ^b Dimensione frattale della curva del drago
^ Stephen Wolfram, Geometry of Binomial Coefficients (1984), su stephenwolfram.com. URL consultato il 29 dicembre 2006 (archiviato dall'url originale il 15 ottobre 2012).
^ P. Ramachandrarao, A. Sinha et D. Sanyal, On the fractal nature of Penrose tiling [1] (PDF)
^ M. Borkovec, W. De Paris et R. Peikert, The Fractal Dimension of the Apollonian Sphere Packing [2] (PDF)
^ G. F. Lawler, O. Schramm, W. Werner, The Dimension of the Planar Brownian Frontier is 4/3 [3] Archiviato il 28 settembre 2007 in Internet Archive. (PDF)
^ ^a ^b ^c Bernard Sapoval, Universalités et fractales, Flammarion, collection Champs (2001), ISBN 2080814664

Bibliografia

¹Kenneth Falconer, Fractal Geometry, John Wiley & Son Ltd; ISBN 0-471-92287-0 (March 1990)
Benoît Mandelbrot, The Fractal Geometry of Nature, W. H. Freeman & Co; ISBN 0-7167-1186-9 (September 1982).
Heinz-Otto Peitgen, The Science of Fractal Images, Dietmar Saupe (éditeur), Springer Verlag, ISBN 0-387-96608-0 (August 1988)
Michael F. Barnsley, Fractals Everywhere, Morgan Kaufmann; ISBN 0-12-079061-0
Bernard Sapoval, « Universalités et fractales », collection Champs, Flammarion.

Voci correlate

Altri progetti

Wikimedia Commons

Wikimedia Commons contiene immagini o altri file su lista di frattali per dimensione di Hausdorff

Collegamenti esterni

The fractals on Mathworld ^{[collegamento interrotto]}, su mathworld.wolfram.com.
Other fractals on Paul Bourke's website, su local.wasp.uwa.edu.au. URL consultato il 29 dicembre 2006 (archiviato dall'url originale il 5 settembre 2006).
Soler's Gallery, su soler7.com.
Fractals on mathcurve.com, su mathcurve.com.
1000fractales.free.fr - Project gathering fractals created with various softwares, su 1000fractales.free.fr.
Fractals unleashed, su library.thinkquest.org. URL consultato il 29 dicembre 2006 (archiviato dall'url originale il 23 settembre 2006).

V · D · M Teoria del caos
Teoria delle biforcazioni	Biforcazione a forcone · Biforcazione a nodo sella · Biforcazione imperfetta · Biforcazione transcritica · Biforcazione di Hopf · Larva del pino (sistema dinamico)
Frattali	Arte frattale · Buddhabrot · Burning ship · Compressione frattale · Curva di Koch · Curva di Peano · Curva di Sierpiński · Dimensione di Hausdorff · Dimensione frattale · Funzione di Cantor · Insieme di Cantor · Insieme di Julia · Insieme di Mandelbrot · Frattali per dimensione di Hausdorff · Polvere di Cantor · Sterling · Triangolo di Sierpiński · Dimensione di Minkowski-Bouligand
Attrattori	Attrattore di Lorenz · Attrattore di Hénon · Mappa di Poincaré · Mappa logistica · Mappa a ferro di cavallo · Spazio delle fasi
Teorici del caos	Edward Norton Lorenz · Aleksandr Michajlovič Ljapunov · Benoît Mandelbrot · Edward Ott · Henri Poincaré · David Ruelle · Stephen Wolfram · James Yorke