ルンゲ＝レンツベクトル

物理学において、ルンゲ＝レンツベクトル（英: Runge–Lenz vector）とは、ケプラー問題、すなわち逆二乗則に従う中心力の下の運動における保存量の一つ[1][2][3]。古典力学の天体運行のケプラー問題や量子力学の水素原子モデルの問題などに現れる。空間的な回転対称性の下で保存量となる角運動量のように、他の多くの保存量が幾何学的な対称性から導かれるのとは異なり、ルンゲ＝レンツベクトルを導く対称性は力学的性質に由来し、力学的対称性と呼ばれる[2][3]。水素原子の束縛状態においては、量子力学的な角運動量演算子とルンゲ＝レンツベクトル演算子の交換関係は4次特殊直交群SO(4)に対応するリー代数をなし、固有値問題の代数的な解法を与える。

ルンゲ＝レンツベクトルという名はドイツの物理学者カール・ルンゲとヴィルヘルム・レンツ（英語版）に因む[4]。1924年の前期量子論の論文において、レンツはケプラー問題の摂動にルンゲ＝レンツベクトルを適用し、その引用文献として、ルンゲのベクトル解析の著作 "Vectoranalysis" を挙げた[5][6]。なお、フランスの物理学者ピエール＝シモン・ラプラスはルンゲやレンツに先駆けて、1799年の天体力学の著作 "Traité de mécanique céleste" の中でルンゲ＝レンツベクトルの性質を論じており[4][7][8]、ラプラス＝ルンゲ＝レンツベクトル（英: Laplace–Runge–Lenz vector）とも呼ばれる。但し、その発見はさらに古く、少なくとも18世紀初頭のベルヌーイ家の門弟ヤコブ・ヘルマン（英語版）とヨハン・ベルヌーイの結果に遡るとされる[9]。

導入

ルンゲ＝レンツベクトルは距離に反比例する引力型の中心力ポテンシャルによるケプラー問題に現れる[1][2][3]。重力ポテンシャルによって太陽の回りを運行する惑星やクーロンポテンシャルによって原子核の回りを運動する水素型原子の電子の運動はそうした例である。ここで、古典力学でのケプラー問題を考え、ルンゲ＝レンツベクトルを導入する。惑星や電子の質量に対し、太陽や原子核の質量は十分大きく、その運動は無視できるとし、原点に固定されているものと仮定する[注 1]。惑星や電子に対応する質点の位置座標を r、質量を m とし、原点を中心とした中心力ポテンシャルを

V ( r ) = − k r ( k > 0 ) {\displaystyle V(r)=-{\frac {k}{r}}\quad (k>0)}

とする。正の定数 k は、重力ポテンシャルの下での天体運行モデルの場合、太陽の質量を M、惑星の質量を m とすれば、万有引力定数 G により、k = GMm で与えられる。また、クーロンポテンシャルの下での水素型原子モデルの場合、原子番号（陽子数）Z、電気素量 e と真空の誘電率 ε0 によって k = Ze2/4πε0 で与えられる[注 2]。このとき、質点の運動を記述する運動方程式は

p ˙ = − ∇ V ( r ) = − k r 2 r r {\displaystyle {\dot {\boldsymbol {p}}}=-\nabla V(r)=-{\frac {k}{r^{2}}}{\frac {\boldsymbol {r}}{r}}}

となる。但し、ドット記号は時間微分を表し、p は運動量

p = m r ˙ {\displaystyle {\boldsymbol {p}}=m{\dot {\boldsymbol {r}}}}

である。運動方程式の右辺は逆二乗則に従う中心力を表している。

この系では、力学的エネルギー

E = m r ˙ 2 2 + V ( r ) {\displaystyle E={\frac {m{\dot {\boldsymbol {r}}}^{2}}{2}}+V(r)}

と角運動量ベクトル

L = r × p {\displaystyle {\boldsymbol {L}}={\boldsymbol {r}}\times {\boldsymbol {p}}}

は時間に対して不変な保存量となる。ここで、質点は角運動量ベクトルに垂直となる平面内を運動し、その軌道は原点を焦点とする二次曲線となる。特に E < 0 の場合、軌道は楕円軌道となる。楕円軌道の軌道長半径を a、軌道離心率を e とすると

E = − k 2 a {\displaystyle E=-{\frac {k}{2a}}}
L = m k a ( 1 − e 2 ) ( L = | L | ) {\displaystyle L={\sqrt {mka(1-e^{2})}}\quad (L=|{\boldsymbol {L}}|)}

の関係が成り立つ[注 3]。

このとき、

A = p × L − m k r r {\displaystyle {\boldsymbol {A}}={\boldsymbol {p}}\times {\boldsymbol {L}}-mk{\frac {\boldsymbol {r}}{r}}}

で定義されるベクトルをルンゲ＝レンツベクトルと呼ぶ[注 4]。ルンゲ＝レンツベクトルは

A ˙ = 0 {\displaystyle {\dot {\boldsymbol {A}}}={\boldsymbol {0}}}

を満たす保存量である。

一般に中心力ポテンシャルの下での運動は回転対称性から角運動量ベクトルは保存量となり、その軌道は角運動量ベクトルに垂直な一定平面内に限られる。一方で、必ずも軌道が閉じて閉軌道となることは保証されない[注 5]。距離に反比例する中心力ポテンシャル V(r) においても、わずかにその値が揺らぐと近日点と遠日点を結ぶ軸に歳差が生じ、楕円軌道としては閉じない。軌道が閉じる背後には角運動量ベクトルに加えて、別の保存量の存在が示唆されるが、ルンゲ＝レンツベクトルがその保存量となっている[2]。

基本的な性質

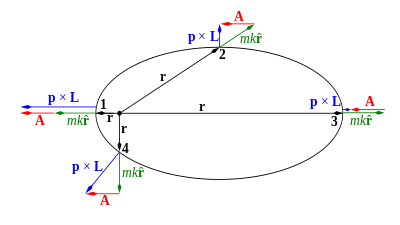
楕円軌道の各点におけるルンゲ＝レンツベクトル A = p × L − mkr/r（赤色の矢印）。ルンゲ＝レンツベクトルは一定であり、その方向は原点から近日点を結ぶベクトル rp と等しく、その大きさは mke である。参考に p × L（青色の矢印）と mkr/r（緑色の矢印）を同時に示している。但し、図中では ˆr = r/r の記法を用いている。

ルンゲ＝レンツベクトルは時間的に変化しない一定ベクトルであり、楕円軌道を含む一定平面内に位置する。その方向は原点である焦点と近日点 (perihelion) を結ぶ方向にある。また、その大きさは

A = m k e {\displaystyle A=mke}

で与えられる。従って、近日点の座標を rp とすると、

A = m k e r p r p {\displaystyle {\boldsymbol {A}}=mke{\frac {{\boldsymbol {r}}_{p}}{r_{p}}}}

と表すことができる。ルンゲ＝レンツベクトルを mk で除したベクトル

e = A m k {\displaystyle {\boldsymbol {e}}={\frac {\boldsymbol {A}}{mk}}}

は大きさが軌道離心率 e である一定ベクトルである。このベクトルは離心率ベクトルと呼ばれる。

ある時刻 t における系の状態は、位置座標 r = (x, y, z) と運動量 p = (px, py, pz) の6つの座標で表される6次元の相空間の点として記述され、その時間発展は相空間上の軌道を描く。一般に保存量が存在すれば、相空間の軌道は制限され、自由度が下がる。特に相空間の次元を 2n とすると n 個の独立な保存量が存在すれば、相空間上の軌道は完全に決定される[注 6]。ケプラー問題において、エネルギーと角運動量ベクトルの3成分、ルンゲ＝レンツベクトルの3成分は保存量である。その総数は7個であり、相空間の次元6より多い。このことはルンゲ＝レンツベクトルと角運動量ベクトル、エネルギーは互いに独立ではないことを意味する。実際、ルンゲ＝レンツベクトルと角運動量ベクトルは直交しており、

A ⋅ L = 0 {\displaystyle {\boldsymbol {A}}\cdot {\boldsymbol {L}}={\boldsymbol {0}}}

を満たす。また、ルンゲ＝レンツベクトル、角運動量ベクトル、エネルギーは関係式

A 2 = m 2 k 2 + 2 m E L 2 {\displaystyle A^{2}=m^{2}k^{2}+2mEL^{2}}

で結ばれている。

歴史

ルンゲ＝レンツベクトルという名はドイツの物理学者カール・ルンゲとヴィルヘルム・レンツ（英語版）に因む。レンツは前期量子論でケプラー問題を扱った1924年の論文の中で、エネルギー準位の摂動にルンゲ＝レンツベクトルを適用した[5]。そして、引用文献として、ルンゲの著作 "Vectoranalysis" を挙げた。ルンゲはその著作において、ベクトルが関わる微積分を扱った章で、中心力の下での運動では角運動量が保存量となることを示した後、距離の2乗に反比例する中心力では別の定ベクトルが存在し、逆にその定ベクトルから軌道の方程式が導かれることを記している[6]。但し、参照文献を記しておらず、それが誰の発見によるものかも述べていない。その後、物理学者ヴォルフガング・パウリは、1926年の論文で当時、原子構造を説明する新しい理論として発展しつつあった行列力学を水素原子に適用し、その中でレンツの結果を引用した[10]。パウリはこの論文の中で、ルンゲ＝レンツベクトルを足掛かりに、行列力学によって、水素原子のスペクトル構造や外部電場を印加した時のシュタルク効果による補正を導いた。ルンゲ＝レンツベクトルについては、パウリは「レンツによって用いられた」とのみ述べているが、その後、物理学ではルンゲ＝レンツベクトルの名で定着するに至った[4]。

なお、ルンゲとレンツの名を冠するルンゲ＝レンツベクトルだが、その発見の歴史はさらに時代を遡り、また、何度か独立に再発見されてきた[4][9]。多くの現代的な天体力学の文献は、ルンゲ＝レンツベクトルの発見をフランスの物理学者ピエール＝シモン・ラプラス、または四元数を発見したことで知られるアイルランドの数学者ウィリアム・ローワン・ハミルトンによるものとしている[4]。ラプラスは、1799年の天体力学の著作 "Traité de mécanique céleste" の第1巻において、ルンゲ＝レンツベクトルに相当する保存量を導いている。ラプラスは楕円軌道となる天体の運動を論じた章の中で、エネルギー、角運動量ベクトル、ルンゲ＝レンツベクトルに相当する7個の第一積分を導き、さらにこれらのうち、5個だけが独立であることを指摘している[7][8]。一方、ハミルトンは、1843年の四元数の発見後、精力的に理論の普及活動と諸分野への応用を行ったが、アイルランド王立アカデミー（英語版）に送った1847年の四元数を力学に応用した論文の中で、ルンゲ＝レンツベクトルに相当する離心率ベクトルを独立に導いている[11]。

ハミルトン形式とポアソン括弧

ハミルトン形式の解析力学で記述すれば、ケプラー問題の対称性とルンゲ＝レンツベクトルの性質がより明らかになる[12]。角運動量ベクトル L = (L1, L2, L3) の各成分同士のポアソン括弧は

{ L 1 , L 2 } = L 3 , { L 2 , L 3 } = L 1 , { L 3 , L 1 } = L 2 {\displaystyle \{L_{1},L_{2}\}=L_{3},\,\{L_{2},L_{3}\}=L_{1},\,\{L_{3},L_{1}\}=L_{2}}

という3次特殊直交群SO(3)に対応する関係式を満たす。ここでエディントンのイプシロン εijk を用いれば、

{ L i , L j } = ∑ k = 1 3 ϵ i j k L k {\displaystyle \{L_{i},L_{j}\}=\sum _{k=1}^{3}\epsilon _{ijk}L_{k}}

と表すことができる。また、角運動量ベクトルとルンゲ＝レンツベクトルのポアソン括弧は

{ A i , L j } = ∑ k = 1 3 ϵ i j k A k {\displaystyle \{A_{i},L_{j}\}=\sum _{k=1}^{3}\epsilon _{ijk}A_{k}}

となる。一方、ルンゲ＝レンツベクトル同士のポアソン括弧は、例えば

{ A 1 , A 2 } = − ( p 2 − 2 m k r ) L 3 = − 2 m E L 3 {\displaystyle \{A_{1},A_{2}\}=-\left(p^{2}-{\frac {2mk}{r}}\right)L_{3}=-2mEL_{3}}

となり、定数項 −2mE の係数が付く。ここで E < 0 となる束縛状態について

D = A − 2 m E {\displaystyle {\boldsymbol {D}}={\frac {\boldsymbol {A}}{\sqrt {-2mE}}}}

を導入すれば、

{ L i , L j } = ∑ k = 1 3 ϵ i j k L k {\displaystyle \{L_{i},L_{j}\}=\sum _{k=1}^{3}\epsilon _{ijk}L_{k}}
{ D i , L j } = ∑ k = 1 3 ϵ i j k D k {\displaystyle \{D_{i},L_{j}\}=\sum _{k=1}^{3}\epsilon _{ijk}D_{k}}
{ D i , D j } = ∑ k = 1 3 ϵ i j k L k {\displaystyle \{D_{i},D_{j}\}=\sum _{k=1}^{3}\epsilon _{ijk}L_{k}}

と簡明にまとめられる。この関係式はSO(3)を拡大したSO(4)に対応付けられる。

水素型原子モデル

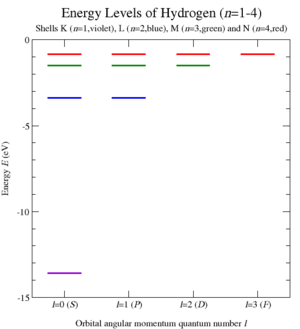
水素原子 (Z = 1) のエネルギー準位。エネルギー固有状態は主量子数 n、方位量子数 l、磁気量子数 m で指定されるが、エネルギー準位は主量子数だけで定まり、n2 重に縮退している。エネルギー準位は角運動量とルンゲ＝レンツベクトルから代数的に求めることができる。

量子力学においては、対称性は保存量と結び付き、エネルギー準位の縮退を導く。水素型原子モデルのエネルギー固有状態は主量子数 n、方位量子数 l、磁気量子数 m で指定されるが、エネルギー準位は主量子数だけで定まり、n2 重に縮退している。空間的に球対称な水素型原子モデルでは、SO(3)で表される回転対称性により、角運動量が保存量となる。但し、回転対称性だけでは −l, −l + 1, …, 0, …, l − 1, l の値をとる磁気量子数による (2l + 1) 重の縮退しか説明できない。このことは、さらに別の対称性の存在を示唆する。この対称性こそが、束縛状態で角運動量とルンゲ＝レンツベクトルがなすSO(4)の対称性である。

量子化

量子力学では正準量子化により、力学的な物理量はエルミート演算子になる。演算子（の各座標成分）同士の積は可換とは限らず、古典力学とは違い演算子 ˆp × ˆL は −ˆL × ˆp に一致しない[注 7]。したがって、ˆp × ˆL はエルミート演算子ではなく[注 8]、量子力学では物理量を表わさない。そこで量子力学的なルンゲ＝レンツベクトルは、エルミート演算子

A ^ = 1 2 ( p ^ × L ^ − L ^ × p ^ ) − m k r ^ r {\displaystyle {\hat {\boldsymbol {A}}}={\frac {1}{2}}({\hat {\boldsymbol {p}}}\times {\hat {\boldsymbol {L}}}-{\hat {\boldsymbol {L}}}\times {\hat {\boldsymbol {p}}})-mk{\frac {\hat {\boldsymbol {r}}}{r}}}

で定義される。

ˆA はハミルトニアン ˆH と可換であるから、ハイゼンベルク方程式からの帰結として保存量であるといえる。

i ℏ d A ^ d t = [ A ^ , H ^ ] = 0 {\displaystyle i\hbar {\frac {\mathrm {d} {\hat {\boldsymbol {A}}}}{\mathrm {d} t}}=[{\hat {\boldsymbol {A}}},\,{\hat {H}}]=0}

また、古典論での関係式に類似した下記の関係を満たす。

A ^ ⋅ L ^ = L ^ ⋅ A ^ = 0 {\displaystyle {\hat {\boldsymbol {A}}}\cdot {\hat {\boldsymbol {L}}}={\hat {\boldsymbol {L}}}\cdot {\hat {\boldsymbol {A}}}=0}
A ^ 2 = m 2 k 2 + 2 m H ^ ( L ^ 2 + ℏ 2 ) {\displaystyle {\hat {\boldsymbol {A}}}^{2}=m^{2}k^{2}+2m{\hat {H}}({\hat {\boldsymbol {L}}}^{2}+\hbar ^{2})}

対称性

古典論と同様に E < 0 となる束縛状態について、

D ^ = A ^ − 2 m E {\displaystyle {\hat {\boldsymbol {D}}}={\frac {\hat {\boldsymbol {A}}}{\sqrt {-2mE}}}}

を導入すれば、ˆL との交換関係として、SO(4)に対応する

[ L ^ i , L ^ j ] = i ℏ ∑ k = 1 3 ϵ i j k L ^ k {\displaystyle [{\hat {L}}_{i},{\hat {L}}_{j}]=i\hbar \sum _{k=1}^{3}\epsilon _{ijk}{\hat {L}}_{k}}
[ D ^ i , L ^ j ] = i ℏ ∑ k = 1 3 ϵ i j k D ^ k {\displaystyle [{\hat {D}}_{i},{\hat {L}}_{j}]=i\hbar \sum _{k=1}^{3}\epsilon _{ijk}{\hat {D}}_{k}}
[ D ^ i , D ^ j ] = i ℏ ∑ k = 1 3 ϵ i j k L ^ k {\displaystyle [{\hat {D}}_{i},{\hat {D}}_{j}]=i\hbar \sum _{k=1}^{3}\epsilon _{ijk}{\hat {L}}_{k}}

が成り立つ。すなわち、SO(3)またはそれと局所同型なSU(2)に対応していた ˆL の交換関係がなすリー代数は、SO(4)のものに拡張される。さらに、

I ^ = 1 2 ( L ^ + D ^ ) {\displaystyle {\hat {\boldsymbol {I}}}={\frac {1}{2}}({\hat {\boldsymbol {L}}}+{\hat {\boldsymbol {D}}})}
K ^ = 1 2 ( L ^ − D ^ ) {\displaystyle {\hat {\boldsymbol {K}}}={\frac {1}{2}}({\hat {\boldsymbol {L}}}-{\hat {\boldsymbol {D}}})}

を導入すると、これらは

[ I ^ i , I ^ j ] = i ℏ ∑ k = 1 3 ϵ i j k I ^ k {\displaystyle [{\hat {I}}_{i},{\hat {I}}_{j}]=i\hbar \sum _{k=1}^{3}\epsilon _{ijk}{\hat {I}}_{k}}
[ K ^ i , K ^ j ] = i ℏ ∑ k = 1 3 ϵ i j k K ^ k {\displaystyle [{\hat {K}}_{i},{\hat {K}}_{j}]=i\hbar \sum _{k=1}^{3}\epsilon _{ijk}{\hat {K}}_{k}}
[ I ^ i , K ^ j ] = 0 {\displaystyle [{\hat {I}}_{i},{\hat {K}}_{j}]=0}
[ I ^ , H ^ ] = [ K ^ , H ^ ] = 0 {\displaystyle [{\hat {\boldsymbol {I}}},{\hat {H}}]=[{\hat {\boldsymbol {K}}},{\hat {H}}]=0}

と独立な2つのSO(3)またはSU(2)に付随したリー代数をなす。したがって、角運動量演算子の場合と同様にハミルトニアンを同時対角化する ˆI2, ˆK2 の固有値の取りうる値は

I ^ 2 = s ( s + 1 ) ℏ 2 s = 0 , 1 2 , 1 , ⋯ {\displaystyle {\hat {\boldsymbol {I}}}^{2}=s(s+1)\hbar ^{2}\quad s=0,{\frac {1}{2}},1,\cdots }
K ^ 2 = s ′ ( s ′ + 1 ) ℏ 2 s ′ = 0 , 1 2 , 1 , ⋯ {\displaystyle {\hat {\boldsymbol {K}}}^{2}=s'(s'+1)\hbar ^{2}\quad s'=0,{\frac {1}{2}},1,\cdots }

となる。一方、SO(4)に付随するリー代数は階数2であり、リー代数の全ての元と可換となるカシミール演算子（英語版）は2つ存在するが

I ^ 2 = 1 4 ( L ^ + D ^ ) 2 {\displaystyle {\hat {\boldsymbol {I}}}^{2}={\frac {1}{4}}({\hat {\boldsymbol {L}}}+{\hat {\boldsymbol {D}}})^{2}}
K ^ 2 = 1 4 ( L ^ − D ^ ) 2 {\displaystyle {\hat {\boldsymbol {K}}}^{2}={\frac {1}{4}}({\hat {\boldsymbol {L}}}-{\hat {\boldsymbol {D}}})^{2}}

が該当する。

エネルギー準位

カシミール演算子としては、ˆI2, ˆK2 の線形結合として

C 1 ^ = I ^ 2 + K ^ 2 = 1 2 ( L ^ 2 + D ^ 2 ) {\displaystyle {\hat {C_{1}}}={\hat {\boldsymbol {I}}}^{2}+{\hat {\boldsymbol {K}}}^{2}={\frac {1}{2}}({\hat {\boldsymbol {L}}}^{2}+{\hat {\boldsymbol {D}}}^{2})}
C 2 ^ = I ^ 2 − K ^ 2 = L ^ ⋅ D ^ {\displaystyle {\hat {C_{2}}}={\hat {\boldsymbol {I}}}^{2}-{\hat {\boldsymbol {K}}}^{2}={\hat {\boldsymbol {L}}}\cdot {\hat {\boldsymbol {D}}}}

をとることができる。ここで、ˆL·ˆD = 0 であるから、SO(4)のなすリー代数を ˆI2 = ˆK2 に制限してよい。よって、s = s′ であり、ˆC1 のとり得る値は

C 1 ^ = 2 s ( s + 1 ) ℏ 2 {\displaystyle {\hat {C_{1}}}=2s(s+1)\hbar ^{2}}

となる。一方、

C 1 ^ = 1 2 ( L ^ 2 − 1 2 m E A ^ 2 ) = − m k 2 4 E − 1 2 ℏ 2 {\displaystyle {\hat {C_{1}}}={\frac {1}{2}}\left({\hat {\boldsymbol {L}}}^{2}-{\frac {1}{2mE}}{\hat {\boldsymbol {A}}}^{2}\right)=-{\frac {mk^{2}}{4E}}-{\frac {1}{2}}\hbar ^{2}}

であるから、水素型原子のエネルギー準位は

E = − m k 2 2 ℏ 2 ( 2 s + 1 ) 2 s = 0 , 1 2 , 1 , ⋯ {\displaystyle E=-{\frac {mk^{2}}{2\hbar ^{2}(2s+1)^{2}}}\quad s=0,{\frac {1}{2}},1,\cdots }

となる。ここで、2s + 1 は主量子数 n に対応する。

脚注

[脚注の使い方]

注釈

  1. ^ より厳密に2体問題から導出するならば、重心運動と相対運動を分離し、質点の質量 m の代わりに換算質量、位置座標 r の代わりに相対座標を用いればよい。
  2. ^ 原子核の周りを運動する電子が増えると遮蔽効果が顕著となる。原子番号 Z を有効核電荷 Zeff = Z − σ に置き換えればよい（遮蔽定数 σ）。
  3. ^ 特に断りのない限り、ベクトル a の大きさは a と表記する。
  4. ^ ここでは Goldstein, Safko & Poole Jr. (2001) の定義に従っているが、Schiff (1968) や Greiner & Müller (1994) など他の文献では A を m で割ったベクトルをルンゲ＝レンツベクトルと定義している。
  5. ^ すべての束縛軌道が閉軌道となるのは、距離に反比例する中心力ポテンシャルと距離の二乗に比例する等方的な調和振動ポテンシャルのみであり、ベルトランの定理として知られている。
  6. ^ ここでの独立とは、ハミルトン力学系のポアソン括弧が包合系をなすことを意味する。このとき、リウヴィルの意味で可積分であるといわれる。
  7. ^ たとえば (ˆp × ˆL)1 − (−ˆL × ˆp)1 = (ˆp2ˆL3 − ˆp3ˆL2) + (ˆL2ˆp3 − ˆL3ˆp2) = [ˆp2, ˆL3] − [ˆp3, ˆL2] = [ˆp2, (ˆr1ˆp2 − ˆr2ˆp1)] − [ˆp3, (ˆr3ˆp1 − ˆr1ˆp3)] = [ˆp2, −ˆr2]ˆp1 − [ˆp3, ˆr3]ˆp1 = 2iħˆp1 ≠ 0
  8. ^ (ˆp × ˆL)† = −(ˆL†) × (ˆp†) = −ˆL × ˆp ≠ ˆp × ˆL

出典

  1. ^ a b Goldstein, Safko & Poole Jr. (2001), chapter 3.
  2. ^ a b c d Schiff (1968), chapter 7.
  3. ^ a b c Greiner & Müller (1994), chapter 14.
  4. ^ a b c d e Goldstein, Herbert (1975). “Prehistory of the "Runge–Lenz" vector”. Am. J. Phys. (AAPT) 43 (8): 737-738. Bibcode: 1975AmJPh..43..737G. doi:10.1119/1.9745. ISSN 0002-9505. LCCN 2007-233687. OCLC 1480178. 
  5. ^ a b W. Lenz (December 1924). “Über den Bewegungsverlauf und die Quantenzustände der gestörten Keplerbewegung”. Z. Physik (Springer) 24 (1): 197-207. doi:10.1007/BF01327245. ISSN 0044-3328. OCLC 630219143. 
  6. ^ a b C. Runge (1919) (PDF). Vectoranalysis. Leipzig: S. Hirzel. https://ia601601.us.archive.org/2/items/in.ernet.dli.2015.211863/2015.211863.Vector-Analysis.pdf 
  7. ^ a b P. S. de Laplace (1799) (PDF). Traité de mécanique céleste. Tome I, Livre II, CHAPITRE III. p. 165. https://ia800205.us.archive.org/19/items/traitdemcani01lapl/traitdemcani01lapl.pdf 
  8. ^ a b ピエール＝シモン・ラプラス 著、竹下貞雄 訳『ラプラスの天体力学論』 第1巻、大学教育出版、2012年1月31日、第1部、第2編、第3章頁。ASIN 4864291209。ISBN 978-4-86429-120-0。 NCID BB08125816。OCLC 836362141。全国書誌番号:22052401。ASIN B01C7A1RM0（Kindle版）。http://www.kyoiku.co.jp/17rapurasu/rapurasu.html。 
  9. ^ a b Goldstein, Herbert (1976). “More on the prehistory of the Laplace or Runge–Lenz vector”. Am. J. Phys. (AAPT) 44 (11): 1123-1124. Bibcode: 1976AmJPh..44.1123G. doi:10.1119/1.10202. ISSN 0002-9505. LCCN 2007-233687. OCLC 1480178. 
  10. ^ Pauli, W. (May 1926). “Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik”. Z. Physik (Springer) 36 (5): 336-363. Bibcode: 1926ZPhy...36..336P. doi:10.1007/BF01450175. ISSN 0044-3328. OCLC 630219143. 
  11. ^ Hamilton, WR (1847). “Applications of Quaternions to Some Dynamical Questions” (PDF). Proc. Roy. Irish Acad. (Royal Irish Academy) 3: Appendix III. pp.xxxvi-l. http://emis.ams.org/classics/Hamilton/DynQue.pdf. 
  12. ^ Goldstein, Safko & Poole Jr. (2001), chapter 9.

参考文献

  • Goldstein, Herbert; Safko, John L.; Poole Jr., Charles P. (June 25, 2001). Classical mechanics (3rd ed.). Addison Wesley. ASIN 0201657023. ISBN 0201657023. NCID BA54224901. OCLC 300293270 
  • Greiner, Walter; Müller, Berndt (November 1994). Quantum Mechanics: Symmetries (2nd Revised ed.). Springer. ASIN 0387580808. ISBN 0387580808. NCID BA23847513. OCLC 61905638 
  • Schiff, Leonard I. (1968). Quantum mechanics (3rd ed.). McGraw-Hill. ASIN B000OG2UB2 

関連項目

外部リンク

  • 法則の辞典『ルンゲ‐レンツ‐パウリのベクトル』 - コトバンク