振幅偏移変調

変調方式
アナログ変調
AM | SSB | FM | PM
デジタル変調
OOK | ASK | PSK | FSK | QAM | APSK（英語版）
DM | MSK | CCK | CPM（英語版） | OFDM | TCM（英語版）
パルス変調
PWM | PAM | PDM | PPM | PCM
スペクトラム拡散
FHSS | DSSS
関連項目
復調
  • 表
  • 話
  • 編
  • 歴

振幅偏移変調（しんぷくへんいへんちょう）もしくは振幅シフトキーイング（しんぷくシフトキーイング、英語: amplitude-shift keying、略号：ASK）はデジタル信号送受信の際に使用する変調方式の1つで、送信データのビット列に対応して搬送波の振幅を変化させることで送信データを送る方式である。日本においては一般にASKと呼ばれる。日本総務省の文書等ではASK変調方式と書かれる。

アナログ変調方式の振幅変調(AM)と同様に、この変調方式は、他の変調方式と比べて、ノイズや妨害波やフェージングの影響を受けやすい。

この変調方式では、搬送波の周波数と位相はそのままで、搬送波の振幅のみ変化する。単純な2値ASKの場合、デジタル信号が0で振幅小、デジタル信号が1で振幅大とする。

さらに最も単純なものとして、搬送波をスイッチ等で離散的にオン/オフする場合を考えることができる。この場合、デジタル信号が0で搬送波オフ、デジタル信号が1で搬送波オンとする。これはその動作から、オンオフ変調（OOK）と呼ばれている。ただし、大抵の場合、ASKとOOKは明確に区別されず、単にASKと呼ばれる。OOKの変調及び復調装置は他の変調方式の装置と比べて、それほど複雑・高価なものではない。そのため、OOKの技術は、光ファイバーでデータ送信を行なう場合に一般に使用されている。LED送信器はバイナリーの1が短い光パルス照射、0が光消灯を表す。レーザ送信機は、通常、低い光度の光を放射する様に電流を固定する。この低い光度がバイナリーの0を表し、高い光度レベルがバイナリーの1を表す。

符号化

最も単純で一般的なASKの使用形態は、スイッチにより搬送波が存在する場合をバイナリーの1、存在しない場合をバイナリーの0として表す方法である。この形の変調方法はオンオフ変調と呼ばれており、モールス信号を無線周波数で送信する際にも使用される（CW：連続波を参照）。

更に複雑な符号化では、複数のデータ(ビット)をグループにして、振幅の違いとして表す方法がある。例えば、4段階の振幅の違いでは、各変調波形で2ビットを表すことができ（4値ASK）、8段階の振幅の違いでは3ビットを表すことが可能（8値ASK）である。これは、PSKにおけるQPSKや8PSKと同様の手法である。信号に沢山ビットを詰め込むことで伝送効率を上げることが可能であるが、正確に復号するためには高いS/N比が必要となる。

ここに、振幅偏移変調で使用する送受信システムの典型的な例をダイアグラムで示す。

図は3つのブロックに分けられる。1つ目は送信部。2つ目は線形化した送信経路のモデル、3つ目が受信部であり、各ブロックでは、次の表記が使用される。

  • ht(t) ：送信時の搬送波
  • hc(t) ：送信経路のインパルス応答
  • n(t) ：送信経路へのノイズ
  • hr(t) ：受信機のフィルタ
  • L ：送信時に使用される振幅のレベル数
  • Ts ：2つのシンボルの作成にかかる時間

異なるシンボルは異なる電圧で表される。最大の電圧値をAで表すとすると、全ての電圧値は、[-A,A]の間に入ることになり、次の式で表される。

v i = 2 A L − 1 i − A ; i = 0 , 1 , … , L − 1 {\displaystyle v_{i}={\frac {2A}{L-1}}i-A;\quad i=0,1,\dots ,L-1}

各レベル間の電圧の差は次の式で表される。

Δ = 2 A L − 1 {\displaystyle \Delta ={\frac {2A}{L-1}}}

図において、送信信号のシンボルv[n]が信号源Sでランダムに出力されると考えると、波形生成装置(impulse generator )は、面積v[n]のインパルス波形を作り出す。このインパルス波形はフィルタhtに経由して、チャネルを通して送信される。別の言葉で言えば、各シンボルごとに、対応する振幅の異なる搬送波が送信される。

送信機から出力された信号s(t)は、次の形で表される。

s ( t ) = ∑ n = − ∞ ∞ v [ n ] ⋅ h t ( t − n T s ) {\displaystyle s(t)=\sum _{n=-\infty }^{\infty }v[n]\cdot h_{t}(t-nT_{s})}

受信器で、hr (t)を通してフィルターされた後、信号は、次の形になる。

z ( t ) = n r ( t ) + ∑ n = − ∞ ∞ v [ n ] ⋅ g ( t − n T s ) {\displaystyle z(t)=n_{r}(t)+\sum _{n=-\infty }^{\infty }v[n]\cdot g(t-nT_{s})}

ただし、次の関係がある。

n r ( t ) = n ( t ) ∗ h r ( t ) {\displaystyle n_{r}(t)=n(t)*h_{r}(t)}

g ( t ) = h t ( t ) ∗ h c ( t ) ∗ h r ( t ) {\displaystyle g(t)=h_{t}(t)*h_{c}(t)*h_{r}(t)}

ここで、*は2つの信号の畳み込みを示す。A/D変換後、信号z(k)は、次の形で表される。

z [ k ] = n r [ k ] + v [ k ] g [ 0 ] + ∑ n ≠ k v [ n ] g [ k − n ] {\displaystyle z[k]=n_{r}[k]+v[k]g[0]+\sum _{n\neq k}v[n]g[k-n]}

この関係において、2項目は、復号されるシンボルを表している。 他の項は必要がない項である。第1項はノイズの効果で、第3項目はシンボル間干渉によるものである。

もし、シンボル間(ISI)のナイキスト基準を満たすことのできるg(t)を持つフィルターを選ぶことができれば、シンボル間の干渉は存在せず、合計の値は0となる。したがって、以下の式となる。

z [ k ] = n r [ k ] + v [ k ] g [ 0 ] {\displaystyle z[k]=n_{r}[k]+v[k]g[0]}

この場合、送信信号はノイズのみの影響を受ける。

誤り率

あるシンボルが送信された際にエラーを起こす確率密度関数はガウス関数によりモデル化される。平均値は、送信した値から求められ、その分散は次式で与えられる。

σ N = ∫ − ∞ + ∞ Φ N ( f ) ⋅ | H r ( f ) | 2 d f {\displaystyle \sigma _{N}=\int _{-\infty }^{+\infty }\Phi _{N}(f)\cdot |H_{r}(f)|^{2}df}

ただし、 Φ N ( f ) {\displaystyle \Phi _{N}(f)} は帯域中のノイズのスペクトル密度で、Hr (f)はhr (f)で表されるフィルタのインパルス応答の連続フーリエ変換である。

誤りを生じる確率は次式で与えられる。

P e = P e / H 0 ⋅ P H 0 + P e / H 1 ⋅ P H 1 + ⋯ + P e / H L − 1 ⋅ P H L − 1 {\displaystyle P_{e}=P_{e/H_{0}}\cdot P_{H_{0}}+P_{e/H_{1}}\cdot P_{H_{1}}+\dots +P_{e/H_{L-1}}\cdot P_{H_{L-1}}}

ただし、 P e / H 0 {\displaystyle P_{e/H_{0}}} はシンボルviが送信された後、誤りが生じる条件付き確率であり、 P H 0 {\displaystyle P_{H_{0}}} はシンボルv0を送信する確率である。

もし、全てのシンボルを送信する確率が同一であるなら、次の式のようになる。

P H i = 1 L {\displaystyle P_{H_{i}}={\frac {1}{L}}}

もし、全ての確率密度関数を、送信される電圧のとりうる値に対して、同じ図表上にプロットするのであるなら、次のような図が得られる(下の図はL=4の場合)。

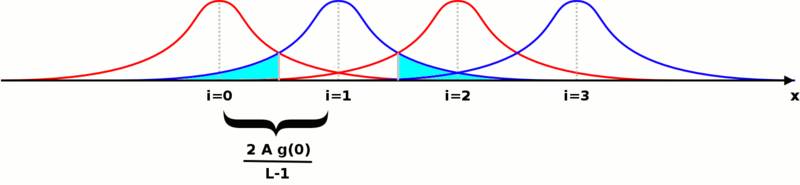
1つのシンボルが送信された後、誤りが生じる確率はガウス分布関数において他のシンボルに対応する振幅となる部分の面積に相当する。これは、図のシアン色の部分である。もし、ガウス分布におけるこの部分の面積1つをP+と定義するなら、合計の面積は 2 L P + − 2 P + {\displaystyle 2LP^{+}-2P^{+}} .となる。したがって、誤り率の合計は次の形で表される。

P e = 2 ( 1 − 1 L ) P + {\displaystyle P_{e}=2\left(1-{\frac {1}{L}}\right)P^{+}}

ここで、P+.の値を計算する。 この計算のためには、基準点を変更する。下に示す関数の面積は変わらない。ここでは、次の図に示す様な状況を考える。

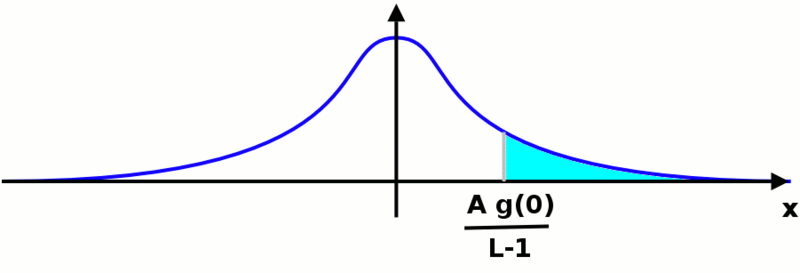
これでは、どの様なガウス分布関数を仮定しようと関係なく、我々が計算する面積は同一となる。我々が求める値は次の積分で与えられる。

P + = ∫ A g ( 0 ) L − 1 ∞ 1 2 π σ N e − x 2 2 σ N 2 d x = 1 2 erfc ⁡ ( A g ( 0 ) 2 ( L − 1 ) σ N ) {\displaystyle P^{+}=\int _{\frac {Ag(0)}{L-1}}^{\infty }{\frac {1}{{\sqrt {2\pi }}\sigma _{N}}}e^{-{\frac {x^{2}}{2\sigma _{N}^{2}}}}dx={\frac {1}{2}}\operatorname {erfc} \left({\frac {Ag(0)}{{\sqrt {2}}(L-1)\sigma _{N}}}\right)}

ただし、erfc()は相補誤差関数である。これらの結果を全てまとめると誤り率は以下の式で表される。

P e = ( 1 − 1 L ) erfc ⁡ ( A g ( 0 ) 2 ( L − 1 ) σ N ) {\displaystyle P_{e}=\left(1-{\frac {1}{L}}\right)\operatorname {erfc} \left({\frac {Ag(0)}{{\sqrt {2}}(L-1)\sigma _{N}}}\right)}

この式より、送信信号の最大振幅を増やすか、系の増幅率を増加させることで、誤り率を低減することが容易に可能であることが分かる。一方でシンボル中のビット数(振幅のレベル数L)を増やしたり、ノイズのパワーが増加すると、誤り率が増加することが分かる。

この関係は、シンボル間の干渉が存在しない場合、すなわち、g(t)がナイキストの関数である場合に有効である。

関連項目

外部リンク

  • Calculating the Sensitivity of an Amplitude Shift Keying (ASK) Receiver(ASK受信機の感度計算)