Funkcja gęstości prawdopodobieństwa

Ten artykuł od 2013-01 wymaga zweryfikowania podanych informacji. Należy podać wiarygodne źródła w formie przypisów bibliograficznych. Część lub nawet wszystkie informacje w artykule mogą być nieprawdziwe. Jako pozbawione źródeł mogą zostać zakwestionowane i usunięte. Sprawdź w źródłach: Encyklopedia PWN • Google Books • Google Scholar • Federacja Bibliotek Cyfrowych • BazHum • BazTech • RCIN • Internet Archive (texts / inlibrary) Dokładniejsze informacje o tym, co należy poprawić, być może znajdują się w dyskusji tego artykułu. Po wyeliminowaniu niedoskonałości należy usunąć szablon {{Dopracować}} z tego artykułu.

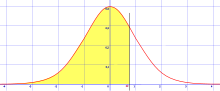
Funkcja gęstości prawdopodobieństwa (gęstość zmiennej losowej) – nieujemna funkcja rzeczywista, określona dla rozkładu prawdopodobieństwa, taka że całka z tej funkcji, obliczona w odpowiednich granicach, jest równa prawdopodobieństwu wystąpienia danego zdarzenia losowego. Funkcję gęstości definiuje się dla rozkładów prawdopodobieństwa jednowymiarowych i wielowymiarowych. Rozkłady mające gęstość nazywane są rozkładami ciągłymi.

Definicja formalna

Niech ${\displaystyle P}$ będzie rozkładem prawdopodobieństwa w przestrzeni ${\displaystyle \mathbb {R} ^{N}}$ (w szczególności na prostej rzeczywistej ${\displaystyle \mathbb {R} }$).

Gęstością rozkładu prawdopodobieństwa ${\displaystyle P}$ nazywa się nieujemną funkcję borelowską ${\displaystyle f\colon \mathbb {R} ^{N}\to \mathbb {R_{+}} \cup \{0\},}$ taką, że dla każdego zbioru borelowskiego ${\displaystyle B\subseteq \mathbb {R} ^{N}}$ zachodzi równość:

${\displaystyle P(B)=\int \limits _{B}f(x)dx,}$

tzn. całka z funkcji ${\displaystyle f}$ obliczona na zbiorze ${\displaystyle B}$ jest równa prawdopodobieństwu ${\displaystyle P(B)}$ przypisanemu zbiorowi ${\displaystyle B.}$

W szczególnych przypadkach konieczne jest użycie całki Lebesgue’a.

Unormowanie gęstości

Tw. 1 (o unormowaniu gęstości) Jeśli ${\displaystyle f}$ jest gęstością rozkładu ${\displaystyle P,}$ to w szczególności, na mocy powyższej definicji:

${\displaystyle \int \limits _{!\mathbb {R} ^{N}}f(x)dx=1,}$

tzn. całka z funkcji gęstości, obliczona na całej przestrzeni ${\displaystyle \mathbb {R} ^{N}}$ jest równa 1.

Tw. 2 (o istnieniu rozkładu dla danej gęstości)

Każda nieujemna funkcja borelowska ${\displaystyle f,}$ spełniająca powyższy warunek, jest gęstością jakiegoś rozkładu prawdopodobieństwa ${\displaystyle P.}$

Gęstość a dystrybuanta – przypadek 1-wymiarowy

Tw. 3 (o obliczaniu dystrybuanty)

Załóżmy, że ${\displaystyle f}$ jest gęstością rozkładu ${\displaystyle P.}$ Wówczas dystrybuantę ${\displaystyle F_{P}}$ rozkładu ${\displaystyle P}$ można wyznaczyć z gęstości

${\displaystyle F_{P}(x)\equiv P(\,\,(-\infty ,x]\,\,)=\int \limits _{-\infty }^{x}f(t)dt.}$

Jeśli więc istnieje gęstość, to za jej pomocą można w prosty sposób wyrazić dystrybuantę rozkładu. Jest to przydatne, gdy dystrybuanty nie daje się wyrazić w sposób elementarny (np. dla rozkładu normalnego).

Tw. 4. Warunkiem koniecznym i wystarczającym na istnienie gęstości dla danego rozkładu ${\displaystyle P}$ jest bezwzględna ciągłość jego dystrybuanty.

Sama ciągłość nie jest warunkiem wystarczającym – istnieją dystrybuanty ciągłe, które nie mają gęstości (np. dystrybuanta Cantora).

Tw. 5. Jeśli ${\displaystyle F}$ jest dystrybuantą, to jest ona prawie wszędzie różniczkowalna oraz jeśli ${\displaystyle F'}$ (określona prawie wszędzie) jest prawie wszędzie różna od zera, to jest ona gęstością.

Gęstość a wartość oczekiwana – przypadek 1-wymiarowy

Tw. 6. Jeżeli ${\displaystyle X}$ jest jednowymiarową zmienną losową o rozkładzie ciągłym z gęstością ${\displaystyle f(x),}$ to jej wartość oczekiwana wyraża się wzorem:

${\displaystyle E(X)=\int \limits _{-\infty }^{\infty }xf(x)dx.}$

Gęstość sumy zmiennych losowych

Tw. 7

a) Jeżeli ${\displaystyle X}$ i ${\displaystyle Y}$ są niezależnymi zmiennymi losowymi oraz przynajmniej jedna ma rozkład ciągły, to ich suma ma rozkład ciągły.

b) Jeśli ponadto obydwie zmienne losowe mają rozkłady ciągłe, to gęstość ich sumy jest splotem ich gęstości.

Własności gęstości – przypadek 2-wymiarowy

Objętość bryły ograniczonej funkcją gęstości

Tw. 8. Objętość bryły ograniczonej od góry funkcją gęstości dwóch zmiennych, a od dołu płaszczyzną ${\displaystyle z=0}$ jest zawsze równe ${\displaystyle 1,}$ tzn.

${\displaystyle \int \limits _{-\infty }^{\infty }\int \limits _{-\infty }^{\infty }f(x,y)\ dy\ dx=1.}$

Wkład do całki z wartości funkcji równych ${\displaystyle 0}$ wynosi ${\displaystyle 0,}$ dlatego można zawęzić powyższe całkowanie do niezerowych obszarów funkcji gęstości. Np. jeśli obszar ten ma postać prostokąta ${\displaystyle [x_{1},x_{2}]\times [y_{1},y_{2}],}$ to

${\displaystyle \int \limits _{x_{1}}^{x_{2}}\int \limits _{y_{1}}^{y_{2}}f(x,y)\ dy\ dx=1.}$

Prawdopodobieństwo wystąpienia wartości z pewnego obszaru płaszczyzny

Aby obliczyć prawdopodobieństwo otrzymania wyniku z pewnego obszaru ${\displaystyle D}$ płaszczyzny, to trzeba dokonać całkowania z funkcji gęstości po tym obszarze, tj.

${\displaystyle P(D)=\iint \limits _{D}f(x,y)\ dy\ dx.}$

Jeżeli np. liczymy sumaryczne prawdopodobieństwo otrzymania wartości należącej do prostokąta ${\displaystyle [x_{1},x_{2}]\times [y_{1},y_{2}],}$ to jest równa wartości całki z funkcji gęstości oznaczonej granicami przedziałów:

${\displaystyle P(x_{1}<X<x_{2},y_{1}<Y<y_{2})=\int \limits _{x_{1}}^{x_{2}}\int \limits _{y_{1}}^{y_{2}}f(x,y)\ dy\ dx.}$

Twierdzenie o niezależności zmiennych losowych

Zmienne losowe ${\displaystyle X,Y}$ posiadające swoje funkcje gęstości

${\displaystyle f_{1}(x)=\int \limits _{-\infty }^{\infty }f(x,y)\ dy,}$

${\displaystyle f_{2}(y)=\int \limits _{-\infty }^{\infty }f(x,y)\ dx.}$

są niezależne, jeżeli funkcja ${\displaystyle f(x,y)}$ jest gęstością wektora losowego ${\displaystyle (X,Y),}$ czyli prawdziwe jest równanie:

${\displaystyle f(x,y)=f_{1}(x)\cdot f_{2}(y).}$

Mechanika kwantowa

W mechanice klasycznej stan układu fizycznego opisuje się np. przez podanie wzajemnych położeń i pędów poszczególnych części układu. Układy fizyczne uznaje się za identyczne, gdy złożone są z takich samych cząstek, mających odpowiednio takie same wzajemne położenia i pędy. Mechanika klasyczna opiera się tu na założeniu, że położenia i pędy można w zasadzie dowolnie dokładnie zmierzyć. Jednak nie jest to prawdą w przypadku, gdy mamy do czynienia z cząstkami o małych masach. W tym wypadku dokładniejszy opis rzeczywistego zachowania się układów fizycznych daje mechanika kwantowa.

W mechanice kwantowej z konieczności rezygnuje się z jednoczesnego przypisywania cząstkom położeń i pędów. W zamian za to stan układu fizycznego opisywany jest za pomocą funkcji falowej. Układy fizyczne są uznawane za identyczne, jeśli przypisuje się im identyczne funkcje falowe. Jednak pomiar wielkości mierzalnej (tzw. obserwabli) przeprowadzany na identycznych układach może prowadzić do różnych wyników. Np. mierząc położenia, pędy, energie cząstek opisywanych taką samą funkcją falową ${\displaystyle \psi (r)}$ otrzymamy wyniki o pewnym rozkładzie losowym, przy tym np. gęstość prawdopodobieństwa znalezienia cząstki w punkcie ${\displaystyle r}$ jest równa kwadratowi modułu funkcji falowej:

${\displaystyle \rho (r)=\psi (r)^{*}\cdot \psi (r)=\left|\psi (r)\right|^{2},}$

gdzie ${\displaystyle ^{*}}$ oznacza sprzężenie zespolone.

W ogólności wyniki każdego pomiaru dokonywanego na identycznych układach są wielowymiarową zmienną losową o określonym rozkładzie prawdopodobieństwa.