Sphenomegacorona

88th Johnson solid (18 faces)

Sphenomegacorona

Type	Johnson J₈₇ – J₈₈ – J₈₉
Faces	16 triangles 2 squares
Edges	28
Vertices	12
Vertex configuration	2(3⁴) 2(3².4²) 2x2(3⁵) 4(3⁴.4)
Symmetry group	C_2v
Dual polyhedron	-
Properties	convex
Net

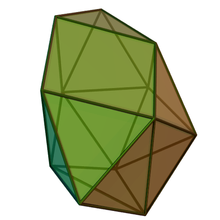
In geometry, the sphenomegacorona is a Johnson solid with 16 equilateral triangles and 2 squares as its faces.

Properties

The sphenomegacorona was named by Johnson (1966) in which he used the prefix spheno- referring to a wedge-like complex formed by two adjacent lunes—a square with equilateral triangles attached on its opposite sides. The suffix -megacorona refers to a crownlike complex of 12 triangles, contrasted with the smaller triangular complex that makes the sphenocorona.^[1] By joining both complexes together, the resulting polyhedron has 16 equilateral triangles and 2 squares, making 18 faces.^[2] All of its faces are regular polygons, categorizing the sphenomegacorona as a Johnson solid—a convex polyhedron in which all of the faces are regular polygons—enumerated as the 88th Johnson solid $J_{88}$ .^[3] It is elementary, meaning it does not arise from "cut-and-paste" manipulations of both Platonic and Archimedean solids.^[4]

The surface area of a sphenomegacorona with edge length a can be calculated as:

A=\left(2+4{\sqrt {3}}\right)a^{2}\approx 8.92820a^{2},

and its volume as

V=\xi a^{3}\approx 1.94811a^{3},

where the decimal expansion of ξ is given by A334114.^[2]^[5]

Cartesian coordinates

Let k ≈ 0.59463 be the smallest positive root of the polynomial

1680x^{16}-4800x^{15}-3712x^{14}+17216x^{13}+1568x^{12}-24576x^{11}+2464x^{10}+17248x^{9}-3384x^{8}-5584x^{7}+2000x^{6}+240x^{5}-776x^{4}+304x^{3}+200x^{2}-56x-23.

Then, Cartesian coordinates of a sphenomegacorona with edge length 2 are given by the union of the orbits of the points

{\begin{aligned}&\left(0,1,2{\sqrt {1-k^{2}}}\right),\,(2k,1,0),\,\left(0,{\frac {\sqrt {3-4k^{2}}}{\sqrt {1-k^{2}}}}+1,{\frac {1-2k^{2}}{\sqrt {1-k^{2}}}}\right),\\&\left(1,0,-{\sqrt {2+4k-4k^{2}}}\right),\,\left(0,{\frac {{\sqrt {3-4k^{2}}}\left(2k^{2}-1\right)}{\left(k^{2}-1\right){\sqrt {1-k^{2}}}}}+1,{\frac {2k^{4}-1}{\left(1-k^{2}\right)^{\frac {3}{2}}}}\right)\end{aligned}}

under the action of the group generated by reflections about the xz-plane and the yz-plane.^[6]

References

^ Johnson, N. W. (1966). "Convex polyhedra with regular faces". Canadian Journal of Mathematics. 18: 169–200. doi:10.4153/cjm-1966-021-8. MR 0185507. S2CID 122006114. Zbl 0132.14603.
^ ^a ^b Berman, M. (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute. 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. MR 0290245.
^ Francis, D. (August 2013). "Johnson solids & their acronyms". Word Ways. 46 (3): 177.
^ Cromwell, P. R. (1997). Polyhedra. Cambridge University Press. p. 87. ISBN 978-0-521-66405-9.
^ OEIS Foundation Inc. (2020), The On-Line Encyclopedia of Integer Sequences, A334114.
^ Timofeenko, A. V. (2009). "The non-Platonic and non-Archimedean noncomposite polyhedra". Journal of Mathematical Science. 162 (5): 717. doi:10.1007/s10958-009-9655-0. S2CID 120114341.